aulaEN03 - eletronica24h

Menu principal:

Educacional > Cursos > Eletronica Basica 1

Aula02 Indice de Aulas Aula04

Eletrônica Básica
Aula 03: Diodo de Junção - Retificador de Meia Onda
Referencias

1. Diodo de Junção

   Um diodo é um dispositivo construído a partir de uma junção PN, portanto deixará que a corrente passe somente num único sentido quando adequadamente polarizado (polarização direta), bloqueando a corrente quando a polaridade da tensão inverter (polarização reversa).
Obs: Não iremos detalhar a parte física do diodo, ficando a seu critério buscar essas informações   na bibliografia que é adotada.
A figura 1 mostra   o diodo com a indicação dos dois terminais , anodo(A) e catodo (K), o simbolo, e o diodo em polarização direta e polarização reversa bem como aspecto fisico de diodos comerciais.

( a ) ( b )

( c )

Figura 1 - ( a ) Aspectos construtivos ( b ) Símbolo ) ( c ) aspecto fisico

1.1. Diodo polarizado diretamente

Para o diodo conduzir, mesmo em polarização direta, é necessário que a tensão externa aplicada seja de pelo menos 0,7 V (para vencer a barreira de potencial). Em condução um diodo apresenta uma queda de tensão de aproximadamente 0,7 V (diodo de Si). No circuito da Figura 2 a a corrente no circuito é de aproximadamente 11,3mA, pois como o mesmo está polarizado diretamente a queda de tensão no diodo é 0,7 V e na resistencia 11,3 V, logo a corrente é 11,3V/1k = 11,3 mA.

Figura 2 - Circuito com o diodo polarizado diretamente

1.2. Diodo polarizado reversamente

Com polarização reversa a corrente no diodo será muito baixa (da ordem de nA para diodos de Si), de forma que do ponto de vista prático será zero. Esta corrente reversa também chamada de corrente de fuga só depende de aspectos construtivos (dopagem) e da temperatura (dobra de valor para cada 10 graus de aumento na temperatura). Observe que quando polarizado reversamente toda a tensão da fonte (na Figura 3, 12 V) cairá entre os terminais do diodo, que deverá ter capacidade para suportar essa tensão reversa, caso contrário pode ocorrer um fenômeno chamado de avalanche o que pode levar à destruição do diodo.

Figura 3 - Circuito com o diodo polarizado reversamente

1.3. Equação caracteristica e curva caracteristica

Assim como uma resistencia, o diodo é um bipolo que é caracterizado por um equação caracteristica, i=f(V).

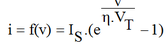
onde

Is corrente reversa de saturação

η (eta) é uma constante que pode variar entre 1 e 2 dependendo de aspectos construtivos do diodo.

VT depende da temperatura cujo valor é calculado por

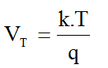
k = constante de Boltzmann T = temperatura ansoluta em kelvin (K) q = carga do eletron em modulo

A Figura 4 mostra a representação grafica da equação caracteristica, a curva caracteristica.

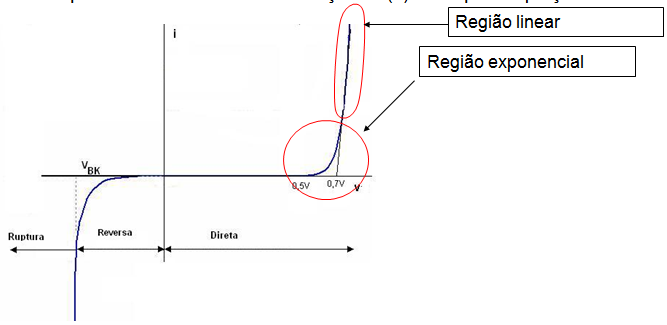
Figura 4 - Curva caracteristica de um diodo de Silicio

Na Figura 4, VBK é a tensão de ruptura ou breakdown, que se atingida provicará a destruição do diodo. Cuidado portanto.

Observe que em polarização direta (anodo positivo em relação ao catodo) a condução efetivamente acontecerá acima de 0,5 V( diodo de Si), que é a tensão de corte.

Observe tambem que existe uma região exponencial e uma região aproximadamente linear. Na região exponencial a corrente é controlada pela barreira de potencial e na região linear a corrente é controlada pela resistencia do diodo.

Na pratica a corrente reversa varia com a tensão pois é constituída de duas componentes: a corrente reversa de saturação (Is) cujo valor só depende da temperatura e da corrente de fuga superficial que depende da tensão aplicada.

1.4. Modelos (circuitos equivalentes) para o diodo

Modelar um dispositivo eletrônico, é usar componentes básicos tais como resistências, fontes de tensão, fontes de corrente e capacitâncias para representa-lo, permitindo desta forma que usar as leis de circuito para estuda-lo. O construtor de um simulador modela um componente eletrônico a partir das informações fornecidas pelo fabricante do componente, desta forma ao simular um circuito os resultados serão semelhantes aos obtidos em um circuito real.

Se voce estudou o curso de Eletricidade Basica compreenderá melhor esse conceito. A Figura 5a mostra uma bateria ligada a uma lampada. Não é possivel calcular a corrente no circuito assim representado, é necessario substituir pelo circuito equivalente ou modelo, Figura 5b. Agora sim é possivel usar leis de circuito para o calculo da corrente.

( a ) ( b )
Figura 5 - ( a ) Circuito a ser modelado ( b ) circuito equivalente da bateria e lampada

1.4.1. Modelo 1 - diodo ideal

O modelo mais simples do diodo considera-o como sendo uma chave que é controlada pela tensão aplicada no diodo. Se a tensão é positiva a chave fecha, se é negativa a chave abre. O diodo se comporta de forma ideal. A Figura 6 mostra a curva caracteristica do diodo assim modelado e o modelo em polarização direta e reversa.

( a ) ( b )

Figura 6 - ( a ) Curva característica do diodo ideal ( b ) circuitos equivalentes na condução (V>0) e corte (V<0)

A Figura 7 mostra dois circuitos, com diodo e com a chave fechada representando o diodo. Como pode ser notado existe uma diferença entre as duas medidas, mas o erro pode ser desprezado.

( a ) ( b )
Figura 7 - ( a ) Circuito com diodo ( b ) circuito com o modelo simplificado (chave fechada)

A pergunta que fica é: Podemos usar esse modelo sempre? Vamos responde-la considerando outro exemplo. Consideremos que a bateria do circuito da Figura 7 muda de valor, passando a valer 3 V. Resulta o circuito da Figura 8.

( a ) ( b)
Figura 8 - ( a ) Circuito com diodo ( b ) circuito com o modelo simplificado (ideal) é inadequado (erro grande)

Observe que neste caso o erro entre as duas corrente é de aproximadamente 20% . Neste caso não podemos mais usar o modelo da chave fechada para representar o diodo. O modelo deve ser melhorado.

1.4.2. Modelo 2 - Bateria

O modelo anterior pode ser melhorado considerando-se que ao conduzir o diodo pode ser substituido por uma bateria de 0,6 V/0,7 V . Se a tensão aplicada no diodo for maior que 0,6 V/0,7 V o diodo será substituido por uma bateria de 0,6 V/0,7 V . Para uma tensão menor que 0,6 V/0,7 V o diodo será um circuito aberto. Alguns autores usam 0,6 V e outros 0,7 V, não faz diferença significativa na maioria dos casos.

( a ) ( b )

Figura 9 - ( a ) Circuito com diodo ( b ) circuito com o modelo com bateria

A Figura 10 mostra as medidas em um circuito com diodo real e no circuito equivalente com a bateria de 0,6 V/0,7 V substituindo o diodo.

( a ) ( b )
Figura 10 - ( a ) Circuito com diodo ( b ) circuito com o modelo com bateria

Como pode ser observardo os valores são muito próximos. O modelo anterior pode ser melhorado mais ainda se substituirmos o diodo por uma bateria em serie com uma resistência (resistência CC do corpo do diodo) para V>0,6 V.

1.4.3. Modelo 3 - Bateria e Resistência (modelo linearizado por trechos de retas)

A Figura 11 mostra a curva característica linearizada por dois trechos de reta.

( a ) ( a )
Figura 11 - ( a ) Circuito com diodo ( b ) circuito com o modelo com bateria e resistencia do diodo (RD)

A Figura 12 mostra as medidas em um circuito com diodo e no circuito equivalente com a bateria de 0,6 V em serie com uma resistência de 50 Ohms substituindo o diodo.

( a ) ( b )
Figura 12 - ( a ) Circuito com diodo ( b ) circuito com o modelo linearizado por trechos de reta

Observar que os resultados são muito próximos, desta forma o modelo a a ser adotado depende dos valores da bateria e da resistência do circuito. Se a tensão da fonte for muito maior do que 0,6 V podemos usar o modelo simplificado, caso contrario deve ser usado o penúltimo ou o ultimo modelo. A grande dificuldade de usar esse modelo é conhecer o valor da resistencia direta do diodo, por isso mesmo os dois primeiros modelos são mais usados.

1.5. Determinação do ponto quiescente

O ponto quiescente, ponto Q, pode ser determinado analiticamente usando leis de circuito ou graficamente atraves da curva caracteristica. .

1.5.1. Determinação do ponto quiescente usando o modelo (leis de circuito)

O ponto quiescente é o ponto de operação do diodo (corrente e tensão) e pode ser determinado através do modelo, o que permite usar as leis de circuito.

Por exemplo, na Figura 13, se usarmos o modelo 2 (bateria) a corrente pode ser estimada por:

1.5. Determinação do ponto quiescente através da analise gráfica

A Figura 14a mostra um circuito com um gerador de FEM=9 V e resistencia interna Ri= 1 Ohm ligado a uma carga de RL=9 Ohms. A resolução desse circuito é muito simples pois os dois bipolos saõ lineares e o circuito é um circuito serie.

I= 9V/(1+9)Ohms = 1 A é a solução analitica

A solução grafica consiste em representar grafica as duas curvas caracteristicas, a do gerador, U=9 - 1.I e a do receptor (resistor), U=9.I. Os dois graficos representam retas, a intersecção das duas retas representa a solução, Figura 14b.

( a ) ( b )
Figura 14 - Determinando o ponto Q ( a ) circuito ( b ) representação grafica dos dois bipolos

No caso da analise grafica com diodo é necessário dispor da curva característica e desenhar no mesmo gráfico a reta de carga do circuito e a curva do diodo. A intersecção entre a reta de carga e a curva é a solução, Figura 15.

Figura 15 - Determinando graficamente o ponto quiescente de um circuito com diodo

É facil de concluir que a solução analitica é mais simples do que a grafica no caso de dois bipolos lineares. O que acontece quando um dos bipolos é não linear?

Obs: Os valores da Figura 15 não estão em escala, VQ=0,7 V e Vcc=12 V.

2. Experiência: Diodo - Polarização e curva caracteristica

2.1. Abra o arquivo ExpEN1 Polarização do diodo e curva caracteristica identifique os circuitos da Figura 14. Inicie a simulação anotando as correntes e a tensão no diodo para as duas situações indicadas.

Polarização direta

I(calc)=_________ I(med)=________ Vdiodo=_______

Polarização Reversa

IS(modelo)=_________ IS(Med)=________ Vdiodo=_______

Obs: IS(modelo) é a corrente de fuga quer você obtêm quando dá duplo clique no simbolo do diodo e entra no modelo.

( a ) ( b )
Figura 16 - Polarização do diodo experiencia 1 ( a ) direta ( b ) reversa

2.2 . Abra o arquivo ExpEN1 Polarização do diodo e curva caracteristica identifique o circuito da Figura 17. Para cada valor de U da tabela 1 meça a corrente. Com os dados da tabela 1 desenhe o grafico de IxU (curva caracteristica) para isso use papel milimetrado ou use o Excel.

Figura 17 - circuito para obter a curva caracteristica

Tabela 1 - levantando dados para desenhar a curva cacteristica do diodo IdxVd

VD(mV)	300	400	500	550	590	600	640	680	700	730
ID(mA)

3. Experiencia: Modelos do diodo

3.1. Abra o arquivo ExpEN1 Modelos do diodo e identifique o circuito da Figura 18. Inicie a simulação. Meça a corrente no diodo e a corrente no circuito com chave e no circuito com bateria, primeiramente considerando a bateria de 20 V que polariza o diodo. Calcule o erro porcentual entre a medida no diodo e nos circuitos com modelo.

( a ) ( b ) ( c )

Figura 18 - Modelos do diodo ( a ) circuito com diodo ( b ) modelo com chave fechada ( c ) modelo com bateria

I(diodo)=___________ I(modelo chave fechada)=______________ I(modelo bateria)=______________

erro%=_______ (modelo chave fechada - ideal) erro%=_______ (modelo bateria)

3.2. Abra o arquivo ExpEN1 Modelos do diodo e identifique o circuito da Figura 19. Inicie a simulação. Meça a corrente no diodo e a corrente no circuito com chave no circuito com bateria e no circuito com bateria e resistencia. Considere agora a bateria de 2 V que polariza o diodo. Calcule o erro porcentual entre a medida no diodo e nos circuitos com modelo.

( a ) ( b ) ( c ) ( d )
Figura 19 - Modelos do diodo ( a ) circuito com diodo ( b ) modelo com chave fechada ( c ) modelo com bateria ( d ) modelo com bateria de 0,6 V e resistencia de 5 ohms

I(diodo)=_______ I(modelo chave fechada)=_________ I(modelo bateria)=_______I(modelo bateria +resistencia)=______

erro%=_______ (modelo chave fechada - ideal) erro%=_______ (modelo bateria) erro%=_______ (modelo bateria+resistencia)

Aula02 Indice de Aulas Aula04