aulaDS007 - eletronica24h
Menu principal:
aulaDS007
Educacional > Cursos > Digital Sequencial
ELETRÔNICA DIGITAL - CIRCUITOS SEQUENCIAIS
Aula 07: Contadores Sincronos
1 Contador Sincrono com FF JK
Como estudado anteriormente nos contadores assincronos o clock (CK) é aplicado no FF correspondente ao LSB (bit menos significativo (Q0). O clock dos FF seguintes é obtido da saida Q do FF anterior ou da saida complementar, Figura 1.
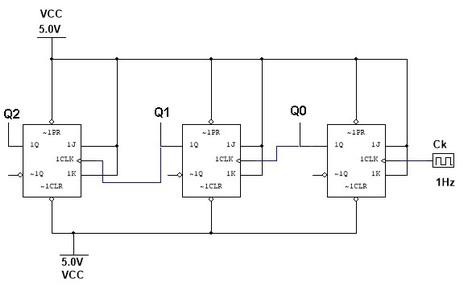
Figura 1 - Contador assincrono de 3 bits
Nos contadores sincronos todos os FF recebem o clock (CK) ao mesmo tempo a principal vantagem é a de poder operar em frequencias mais alta. Alem disso podem executar sequencia qualquer de contagem, Figura 2.
Existe um circuito combinacional que recebe na entrada as saídas Q ou complementar. As saidas desse circuito combinacional serão ligadas nas entradas (J,K,T ou D) dos FF determinando qual o estado futuro (QF) a partir do estado atual (QA). A Figura 2 mostra um circuito genérico.
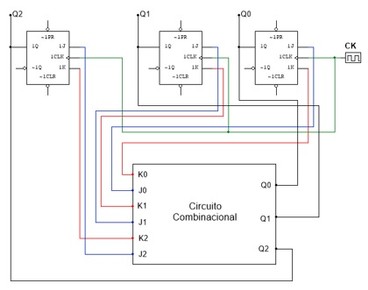
Figura 2 - Contador sincrono de 3 bits generico
Supondo que os FF sejam JK (pode ser T ou D) precisamos relembrar a tabela verdade desse FF, Figura 3.Supondo que os FF sejam JK (pode ser T ou D) precisamos relembrar a tabela verdade desse FF, Figura 3
.Figura 3 - Tabela verdade (TV) do FF JK
1 caso: O estado atual é: QA=0 e desejamos que após o clock QF=0 isso significa que as entradas J e K podem ser: J=K=0 (mantem) ou J=0 e K=1 (impõe 0), isto é, J tem de ser 0, mas K pode ser 0 ou 1, é irrelevante e isso na TV é colocado X.
J K QA QF
0 0 0 → 0 mantem
0 1 0 → 0 impõe 0
0 0 0 → 0 mantem
0 1 0 → 0 impõe 0
Resumindo: as entradas devem ser J=0 e K=X isto é, tanto faz K=0 ou K=1 o estado futuro é 0
2 Caso: Vamos supor que o estado atual é QA=0 e desejamos que após o clock QF=1.
1 0 0 → 1 impõe 1
1 1 0 → 1 complementa
1 1 0 → 1 complementa
Resumindo: as entradas devem ser J=1 e K=X isto é, tanto faz K=0 ou K=1, o estado futuro será 1.
3 Caso: Agora suponha que QA=1 e após o pulso é desejado que QF=0
0 1 1 → 0 impõe 0
1 1 1 → 0 complementa
Resumindo: as entradas devem ser J=X e K=1 isto é, tanto faz J=0 ou J=1, o estado futuro será 0
4 Caso: Agora suponha que QA=1 e após o pulso é desejado que QF=1.
J K QA QF
1 0 1 → 1 impõe 1
1 0 1 → 1 impõe 1
0 0 1 → 1 mantem
Resumindo: as entradas devem ser J=X e K=0, isto é, tanto faz J=0 ou J=1 , o estado futuro será 1.
A partir desses 4 casos e da TV do FF JK, é construida uma tabela que relaciona os estados atual (QA) e futuro (QF) com os valores que devem assumir as entradas J e K, Figura 4.
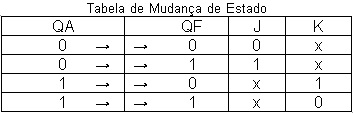
Figura 4 - Tabela de mudança de estado FF JK
Como exemplo de aplicação será construido um contador sincrono de 0 a 7.
2 Contador Sincrono Crescente de 0 a 7
São necessarios 3 FF JK.Os estados costumam ser representados como na Figura 5a, que mostra a sequencia de contagem. Um contador semelhante (0 a 3) ja foi feito de forma assincrona.
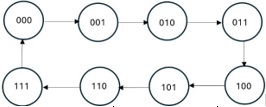
( a ) ( b )
Figura 5 - Contador de 000 a 111 – ( a ) Diagrama de estados ( b ) T.V de mudança de estados
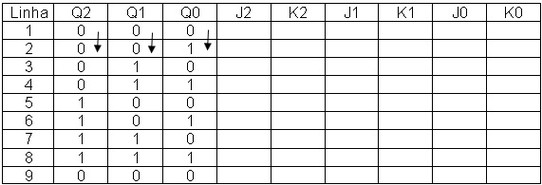
Vamos preencher os valores de J e K da tabela da Figura 5b, usando a tabela 4.
Segunda coluna (Q2), linha 1 da tabela da Figura 5b: QA2=0 QF2=0 de acordo com tabela da Figura 4 J=0 e K=X , isto é, J2=0 e K2=X
Terceira coluna (Q1), linha 1 da tabela da Figura 5b: QA1=0 QF1=0 caso igual ao da primeira coluna logo J1=0 e K1=X
Quarta coluna (Q0), linha 1 da tabela da Figura 5b: QA0=0 QF0=1 de acordo com tabela da Figura 4 J=1 e K=X, isto é, J0=1 e K0=X.
A Figura 6 mostra a tabela da Figura 5b preenchida a linha 1.
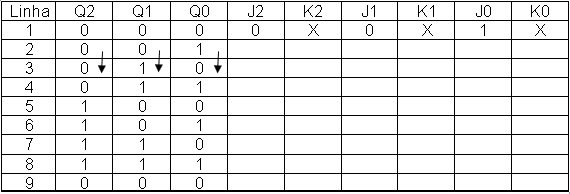
Figura 6 – Tabela da Figura 5b com linha 1 das entradas J K saídas preenchidas
Continuando a preencher as ccolunas de J e K da tabela 6, agora para a linha 2 de acordo com o visto.
Segunda coluna (Q2), linha 2 da tabela da Figura 6: QA2=0 QF2=0 de acordo com tabela da Figura 4 J2=0 e K2=X
Terceira coluna (Q1), linha 2 da tabela da Figura 6: QA1=0 QF1=1 de acordo com tabela da Figura 4 J1=1 e K1=X
Quarta coluna (Q0), linha 2 da tabela da Figura 6: QA0=1 QF0= 0 de acordo com tabela da Figura 4 J0=X e K0=1
A Figura 7 mostra a tabela da Figura 6 preenchida a linha 2.
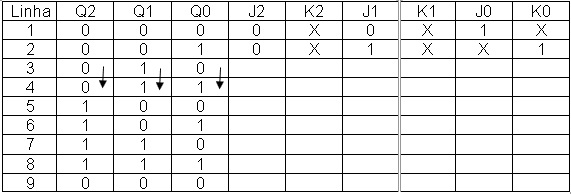
Figura 7 – Tabela da Figura 6 com linha 1, 2 das entradas J K preenchidas
Preenchendo a linha 3 da tabela 7 com os valores de J e K.
A Figura 8 mostra a tabela da Figura 7 preenchida a linha 3
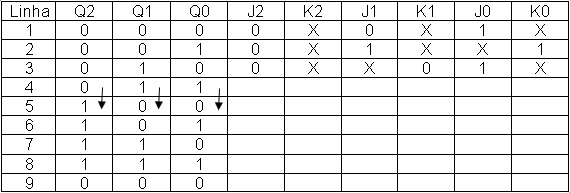
Figura 8 – Tabela da Figura 7 com linhas 1,2, 3 das entradas J K preenchidas
Preenchendo a linha 4 da tabela 8 com os valores de J e K.
Segunda coluna (Q2) e linha 4 da tabela da Figura 8: QA2=0 QF2=1 de acordo com tabela da Figura 4 J2=1 e K2=X
Terceira coluna (Q1) e linha 4 da tabela da Figura 8: QA1=1 QF1=0 de acordo com tabela da Figura 4 J1=X e K1=1
Quarta coluna (Q0) e linha 4 da Tabela da Figura 8: QA0=1 QF0=0 de acordo com tabela da Figura J0=X e K0=1
A Figura 9 mostra a tabela da Figura 8 preenchida a linha 4
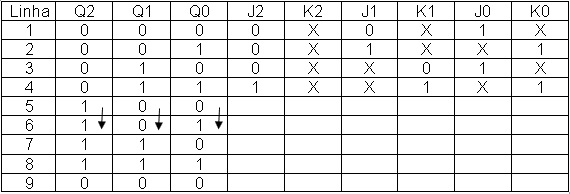
Figura 9 – Tabela da Figura 8 com linhas 1,2,3 e 4 das entradas J K preenchidas
Preenchendo a linha 5 da tabela 9 com os valores de J e K.
A Figura 10 mostra a tabela da Figura 9 preenchida a linha 5
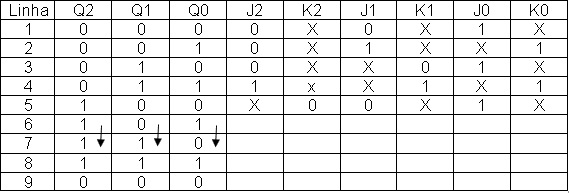
Figura 10 - Tabela da Figura 9 com linhas 1, 2 , 3 ,4 e 5 das entradas J e K preenchidas
Preenchendo a linha 6 da tabela 10 com os valores de J e K.
A Figura 11 mostra a tabela da Figura 10 com a linha 6 preenchida .
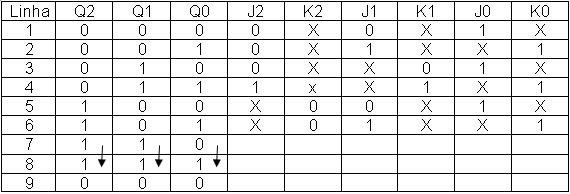
Figura 11 - Tabela da Figura 10 com linhas 1, 2 , 3 ,4, 5 e 6 das entradas J e K preenchidas
Preenchendo a linha 7 da tabela 11 com os valores de J e K.
Terceira coluna (Q1) e linha 7 da tabela da Figura 11: QA1=0 QF1=1 da tabela da Figura 3 J1=X e K1=0
A Figura 12 mostra a tabela da Figura 11 preenchida a linha 7
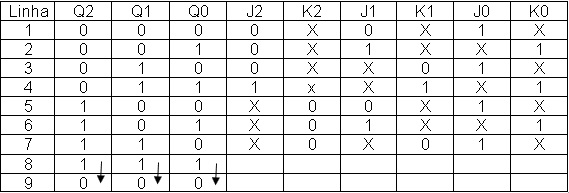
Figura 12 - Tabela da Figura 11 com linhas 1, 2 , 3 ,4, 5, 6 e 7 das saídas preenchidas
Preenchendo a linha 8 da tabela 12 com os valores de J e K.
A Figura 13 mostra a tabela da Figura 12 com a linha 8 preenchida.
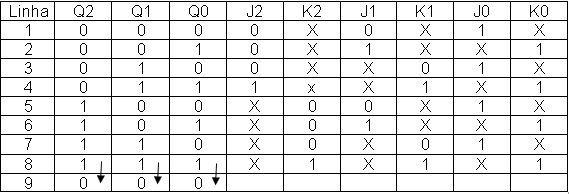
Figura 13 - Tabela da Figura 12 com linhas 1, 2 , 3 ,4, 5, 6, 7 e 8 das saídas preenchidas
Observe que a linha 9 não será preenchida, pois essa mudança de estado já foi feita, linha 1 para linha 2 ou de 000 para 001.
Agora, serão obtidas as expressões booleanas de J=f(Q2,Q1,Q0) e K=f(Q2,Q1,Q0) e para isso será usado o Mapa de Karnaugh que fornece a expressão minimizada.
Obtendo expressão de J2
Os valores de J2 são transportados para um Mapa de Karnaugh de 3 variáveis (Q2Q1Q0) resultando
o gráfico da Figura 14
o gráfico da Figura 14
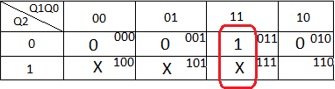
Figura 14 – Mapa de Karnaugh para J2 da Tabela da Figura 13
Do Mapa é obtida a expressão de J2: J2=Q1.Q0
Obtendo a expressão de J1
Os valores de J1 são transportados para um Mapa de Karnaugh de 3 variáveis (Q2Q1Q0) resultando
o gráfico da Figura 16
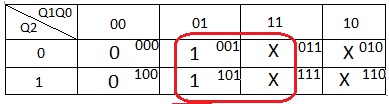
Figura 16 – Mapa de Karnaugh para J1 da Tabela da Figura 13
Do Mapa é obtida a expressão de J1: J1=Q0
Obtendo a expressão de J0
Os valores de J0 são transportados para um Mapa de Karnaugh de 3 variáveis (Q2Q1Q0) resultando
o gráfico da Figura 18
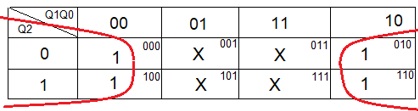
Figura 18 – Mapa de Karnaugh para J0 da Tabela da Figura 13
Do Mapa é obtida a expressão de J0: J0=
Obtendo expressão de K2
Os valores de K2 são transportados para um Mapa de Karnaugh de 3 variáveis (Q2Q1Q0) resultando o
gráfico da Figura 15
gráfico da Figura 15
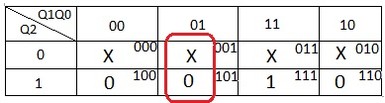
Figura 15 - Mapa de Karnaugh para K2 da Tabela da Figura 13
Do Mapa é obtida a expressão de K2: K2=Q1.Q0
Obtendo a expressão de K1
Os valores de K1 são transportados para um Mapa de Karnaugh de 3 variáveis (Q2Q1Q0) resultando
o gráfico da Figura 17
o gráfico da Figura 17
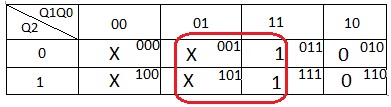
Figura 17 - Mapa de Karnaugh para K1 da Tabela da Figura 13
Do Mapa é obtida a expressão de K1: K1=Q0
Obtendo a expressão de K0
Os valores de K0 são transportados para um Mapa de Karnaugh de 3 variáveis (Q2Q1Q0) resultando
o gráfico da Figura 19
o gráfico da Figura 19
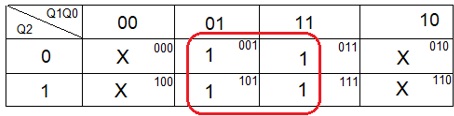
Figura 19 - Mapa de Karnaugh para K0 da Tabela da Figura 13
Do Mapa é obtida a expressão de K0: K1=Q0
Tendo as expressões de J2,K2,J1,K1, J0 e K0 é implementado o circuito do contador de 000 a 111, Figura 20.
Figura 21 - Contador sincrono de 000 a 111
Arquivo Multisim Live - Contador sincrono de 0 a 7
