Teoria de Erros - Introdução - eletronica24h
Menu principal:
Teoria de Erros - Introdução
Links Uteis > Artigos
1. Algarismos Significativos
1.1. Grandeza
Chamamos de grandeza o ente para o qual vale a operação de medir. São exemplos de grandezas: comprimento, tempo, peso, temperatura, área, volume, velocidade, etc.
Medidas das grandezas
“Quando se pode medir aquilo de que se está falando e exprimi-los por números, sabe-se algo a respeito; mas quando não é possível exprimi-lo por número, o conhecimento é escasso e de natureza insatisfatória . Pode ser o inicio do conhecimento, mas não faz avançar senão muito pouco o espírito para o estágio da ciência “
Lord Kelvin
Medir uma grandeza é compara-la com outra fixa,de mesma espécie e considerada como padrão. Após ser feita a comparação , obtemos o que chamamos de medida. Logo: Medição Þ ato de medi
Medida Þ resultado de uma medição.Uma medida é composta de : Medida = (Número)(unidade)
Medida Þ resultado de uma medição.Uma medida é composta de : Medida = (Número)(unidade)
Ex: 0,01mm, 2m, 10g
1.2. Algarismos Significativos
Vamos admitir que se está fazendo a medida usando uma régua milimetrada, como abaixo Qual o valor medido ?

Figura 1 - Efetuando uma medida
Qual o valor da leitura ? 4,34cm ? 4,35cm? Ou 4,36cm?
Das três leituras podemos notar que os algarismos 4 e 3 não são duvidosos porém o terceiro algarismo é. Para saber o número de algarismos significativos , contamos a partir da esquerda para a direita todos os algarismos ( inclusive o duvidoso ), a partir do primeiro diferente de zero.
Exemplos:
a) 15,21m tem 4 AS , sendo 1 o duvidoso
b) 42.020m tem 5 AS sendo o 0 o duvidoso.
c) 25,2s tem 3 AS sendo 1 o duvidoso
d) 25,20s tem 4AS sendo 0 o duvidoso.
e) 25,200s tem 5AS sendo o o duvidoso
Observe que 25,2 ; 25,20 e 25,200 não tem o mesmo significado.
1.3. Arredondamento de AS
Em alguns casos pode ser necessário fazer arredondamentos, eliminando AS. Para fazer arredondamentos usamos a regra :
a) O último algarismo conservado não se altera se o AS eliminado é menor do que 5. :
Ex:
2,422 reduzido a 2AS fica 2,4
25.323 reduzido a 3AS fica 253.102
25.323 reduzido a 2AS fica 25.103
25.323 reduzido a 3AS fica 253.102
25.323 reduzido a 2AS fica 25.103
b) O último AS conservado é acrescido de uma unidade se o AS eliminado for maior ou igual a 5.
Ex:
43,768 reduzido a 4 AS fica 43,77
45.768 reduzido a 2AS fica 46.103
0,0379 reduzido a 2AS fica 0,038
45.768 reduzido a 2AS fica 46.103
0,0379 reduzido a 2AS fica 0,038
1.4. Operações com Algarismos Significativos
a) Adição
Para somar parcelas com AS, devemos inicialmente fazer o arredondamento de modo que todas as parcelas tenham o mesmo numero de casas decimais e igual à da parcela com menos AS.
Ex: Efetuar a soma dos comprimentos
Ex: Efetuar a soma dos comprimentos
12,458cm + 3,22cm + 1,5cm
a ultima parcela é a que tem menos AS logo 12,5cm+3,2cm+1,5cm = 17,2cm
a ultima parcela é a que tem menos AS logo 12,5cm+3,2cm+1,5cm = 17,2cm
b) Subtração
O processo é semelhante à soma.
Ex: 25,482cm – 10,5cm = 25,5 – 10,5 = 15,5cm
c) Multiplicação
O fator que possuir o menor número de AS é que vai determinar o número de AS do resultado.
Ex: 4,62m x 9,3m = 43m2 ( 3ASx2AS =2AS)
1432x2,1 = 3007 = 3,0.103(4ASx2AS=2AS)
1432x2,1 = 3007 = 3,0.103(4ASx2AS=2AS)
d) Divisão
Análogo à multiplicação
Análogo à multiplicação
Ex: 9,2 / 2,31 = 3,98 = 4,0 ( 2AS / 3AS = 2AS )
“ O resultado de um cálculo não pode ser mais preciso que o termo menos preciso envolvido no cálculo “
1.5. Teoria dos Erros
Experiência: Todos os alunos de uma sala de aula medem, com uma régua milimetrada, a maior dimensão de uma mesma caixa de fósforo , anotando os resultados.Com certeza nem todas as medidas tem o mesmo valor, apesar do instrumento de medida ser o mesmo e a grandeza também. Mesmo que o mesmo experimentador repetisse várias vezes as medições , provavelmente os resultados não coincidiriam. Por que isso acontece ?O instrumento o experimentador ou os processos de medição não são perfeitos, logo o resultado não será perfeito. O valor verdadeiro ou absoluto somente será obtido com com instrumentos perfeitos e técnicas perfeitas.
Concluímos que o valor real difere do valor verdadeiro. A esse desvio chamamos de erro da medida ou desvio .
1.5.1. Classificação dos erros
De uma maneira geral , os erros são classificados em :
a) Grosseiros
b) Sistemáticos
c) Acidentais
a) Erros grosseiros : São aqueles causados por falta de atenção ou falta de prática do experimentador.
· Erros de cálculo;
· Erros de leitura ( ler 81 ao invés de 31 );
· Erro de cópia ( transcrever 645 ao inves de 654 );
· Erros provenientes do manuseio errado do instrumento;
· Erro de paralaxe.
Para evitar tais erros deveremos:
Repetir cuidadosamente as medições ( resultados discrepantes devem ser rejeitados )
Adquirir prática com o instrumento medidor.
b) Erros sistemáticos : são conseqüências de imperfeições do instrumento, do experimentador e do método usado.
Instrumento: Deslocamento do zero
Uso de uma escala em condições diferentes daquela em que foi aferida ( em outra temperatura ).
Experimentador: Atrasar ou adiantar o cronômetro.
Experimentador: Atrasar ou adiantar o cronômetro.
Método empregado: negligenciar a ação da temperatura, pressão.
Para evitar tais erros deveremos:
Aferir ou calibrar o instrumento antes do uso.
Substituir a observação humana por elementos mecânicos elétricos ( sensores ).
Escolher um método adequado para aquela medida daquela variável.
Aferir ou calibrar o instrumento antes do uso.
Substituir a observação humana por elementos mecânicos elétricos ( sensores ).
Escolher um método adequado para aquela medida daquela variável.
c) Erros Acidentais: São aqueles provenientes de causas indeterminadas , temporárias, variáveis, imprevisíveis e que modificam de maneira irregular e variável o resultado das medições.Os erros acidentais são inevitáveis , não são elimináveis nem completamente corrigíveis .
A teoria dos erros , fundamentada no cálculo de probabilidades trata dos erros acidentais.
1.5.2. Valor mais provável de uma grandeza (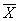 ) ou Valor medio
) ou Valor medio
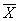 ) ou Valor medio
) ou Valor medioComo não podemos obter a medida verdadeira de uma grandeza , iremos procurar qual o seu valor mais provavel.
Postulado de Gauss:
“para uma série de medidas ( X1,X2,.......XN ) dignas de confiança, o valor mais provável da grandeza,, é a medida aritmética simples de todas as grandezas medidas, isto é :
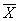 =(X1+X2....+XN)/N
=(X1+X2....+XN)/N1.5.3. Desvio ( d )( resíduo )
Por definição é a diferença entre cada medida encontrada ( X ) e o valor mais provável da grandeza
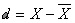
Propriedade :
O desvio pode ser positivo ou negativo.
Para uma quantidade de medidas muito grande a soma dos desvios é nula
Obs: O fato de uma medida ter desvio nulo não significa que ela é “certa “, apenas que, dentro da precisão do aparelho utilizado, não se pode perceber diferenças entre o valor provável e o valor obtido.
Obs: O fato de uma medida ter desvio nulo não significa que ela é “certa “, apenas que, dentro da precisão do aparelho utilizado, não se pode perceber diferenças entre o valor provável e o valor obtido.
1.5.4. Desvio médio absoluto (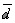 )
)
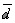 )
)Define-se desvio médio absoluto (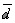 ) para uma série de n medidas como sendo a média aritmética simples dos módulos dos desvios dessas n medidas.
) para uma série de n medidas como sendo a média aritmética simples dos módulos dos desvios dessas n medidas.
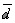 ) para uma série de n medidas como sendo a média aritmética simples dos módulos dos desvios dessas n medidas.
) para uma série de n medidas como sendo a média aritmética simples dos módulos dos desvios dessas n medidas.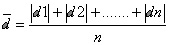
Obs:
1) O desvio médio absoluto deve ser arredondado para um AS.
2) O valor de 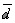 é muito importante, pois, a forma correta de indicar o resultado de uma medição especifica não somente o valor mais provável bem como a incerteza com a qual a medida vem afetada.
é muito importante, pois, a forma correta de indicar o resultado de uma medição especifica não somente o valor mais provável bem como a incerteza com a qual a medida vem afetada.
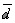 é muito importante, pois, a forma correta de indicar o resultado de uma medição especifica não somente o valor mais provável bem como a incerteza com a qual a medida vem afetada.
é muito importante, pois, a forma correta de indicar o resultado de uma medição especifica não somente o valor mais provável bem como a incerteza com a qual a medida vem afetada.3) O desvio médio é expresso nas mesmas unidades e com a mesma precisão da grandeza que se está medindo.
4) O desvio médio é expresso nas mesmas unidades e com a mesma precisão da grandeza que se está medindo.
O desvio médio absoluto é feito em modulo, pois se levássemos em conta o sinal, alguns positivos se anulariam com alguns negativos, de modo que o desvio médio seria nulo (não teria sentido).
Forma de se indicar corretamente um medida
Valor da medida = 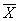
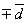
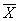
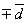
Isto é, indicamos o valor mais provável da medida (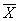 ) e um intervalo de duvida ( ).
) e um intervalo de duvida ( ).
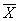 ) e um intervalo de duvida ( ).
) e um intervalo de duvida ( ).1.5.5. Erro Relativo ( er )
Define-se erro relativo ( er ) como sendo a relação entre o desvio médio absoluto e o valor mais provável da grandeza.
Obs: a) É um numero puro b) Esse numero dá uma medida da qualidade da medida, quanto menor for o erro relativo, melhor foi a medida efetuada.
1.5.6. Erro Relativo Porcentual (er%)
Ë o erro relativo expresso em termos de percentagem.

Exercícios Resolvidos
Um grupo de alunos realizou uma série de medições de massa de um corpo, obtendo as seguintes medidas:
M1 =1,45 g M2 =1,43 g M3=1,46 g M4=1,47 g M5=1,49 g
Obter:
a) O valor mais provável da massa do corpo ()
b) Indicar corretamente o resultado final
c) O erro relativo (er)
d) O erro relativo percentual (er%)
| Massa (g) | Desvio(d)(g) | Desvio Absoluto ( 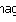 )(g) )(g) | ||
1,45 | ||||
1,43 | ||||
1,46 | ||||
1,47 | ||||
1,49 | ||||
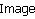 = = | 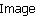 = = | |||
Exercício Proposto
Um grupo de alunos realizou experiência para determinar o valor da aceleração da gravidade local, e obtiveram os valores a seguir:
9,75m/s2; 9,78m/s2;9,80m/s2;9,76m/s2;9,75m/s2
Calcular:
a) valor mais provável da aceleração da gravidade .
b) Indicar corretamente o resultado final .
c) O erro relativo (er)
d) O erro relativo percentual ( er% )