aulaEI04 - eletronica24h
Menu principal:
aulaEI04
Educacional > Cursos > Eletronica Basica 2
1. Multivibrador Astável - Operação
Um astável é um oscilador, e para analisar o seu funcionamento consideremos como ponto de partida (t=0 ) o instante em que o TR1, na Figura 1, estando cortado passa a saturado, ocorrendo o oposto com TR2.
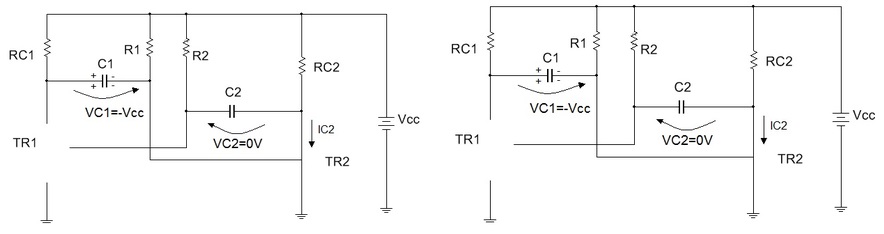
Figura 1 - Multivibrador astável , instante t = 0-.
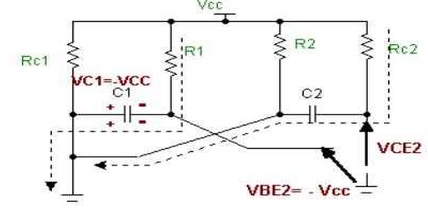
Figura 2 - Circuito no instante t=0+
A partir desse instante ( t=0+) os capacitores começam a se carregar, C1 tende para +VCC (atraves de R1) com constante de tempo t1=R1.C1 e C2 tende para - VCC (de acordo com a polaridade indicada ) com constante de tempo tRec2=RC2.C2
Após um tempo T1 = 0,69.R1.C1 a tensão em C1 começa a ficar positiva fazendo Q2 saturar, enquanto isso, C2 já se carregou com um valor de tensão -VCC (de acordo com a polaridade convencionada). A Fig 3 mostra o circuito após a transição (t = T1+ ) e um pouco antes de mudar (t=T1-).
( a ) (b)
Figura 3 - ( a ) Circuito no instante t=T1- ( b ) Circuito no instante t=T1+
A partir desse instante (t = T1+), C2 tende a se carregar com +VCC com constante de tempo t2= R2.C2 e C1 tenderá para -VCC com constante de tempo tRec1 = RC1.C1 .
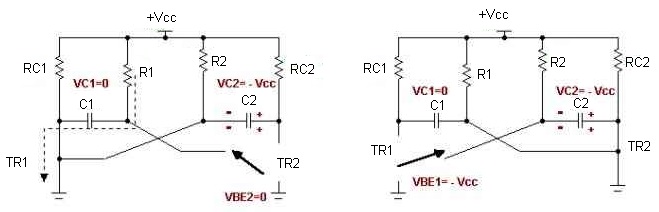
Após um tempo T2 = 0,69.R2.C2 (contado a partir do instante t = T1+) a tensão em C2 começa a ficar positiva fazendo Q1 saturar, enquanto isso C1 já se carregou com -VCC. A Figura 4 mostra o circuito no instante t = (T1 + T2)-. Observe que esse instante é semelhante ao instante t = 0-, isto é, a partir desse instante as situações começam a se repetir e dizemos que foi completado um ciclo ou período.
O período das oscilações é dado por T = T1 + T2 = 0,69.(R2.C2 + R1.C1) . A Figura 5 mostra as principais formas de onda, e podemos observar que as formas de onda são basicamente as mesmas do monoestável.
t = (T1 + T2)-
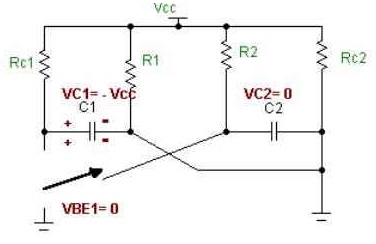
Figura 4 - Circuito com as tensões no instante t=t = (T1 + T2)-
Formas de Onda
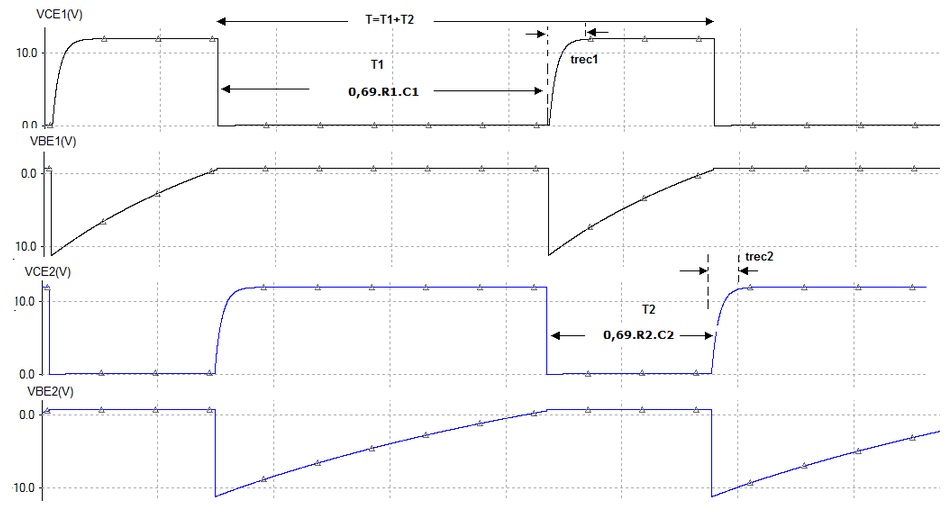
Figura 5 - Formas de onda de VCE1, VBE1, VCE2 e VBE2
No gráfico da Figura 5 as seguintes condições devem ser satisfeitas para que as formas de onda nos coletores não tenha muita distorção:
T1 = 0,69.R1.C1 >> tRec2 = 4.RC2.C2 e T2 = 0,69.R2C2 >> 4.RC1.C1
2. Astável Simétrico
No caso mais comum o astável é simétrico, isto é, T1=T2=T/2 e isso é obtido fazendo-se R1=R2=R e C1=C2=C, de forma que T1=T2 =0,69.R.C e a condição acima para esse caso fica sendo 0,69.R.C > 4.RC.C admitindo que RC1 = RC2 = RC a expressão resulta 5,8.RC<R
Outra condição que deve ser satisfeita é, o transistor que está conduzindo deve estar saturado, e no caso do astável simétrico isso será verdadeiro se for observada a condição: R< bmin.RC
Combinando as duas condições resulta : 5,8.RC < R < bmin.RC
esta desigualdade mais a expressão que dá o período T = 1,38.R.C permitem fazer facilmente qualquer projeto.
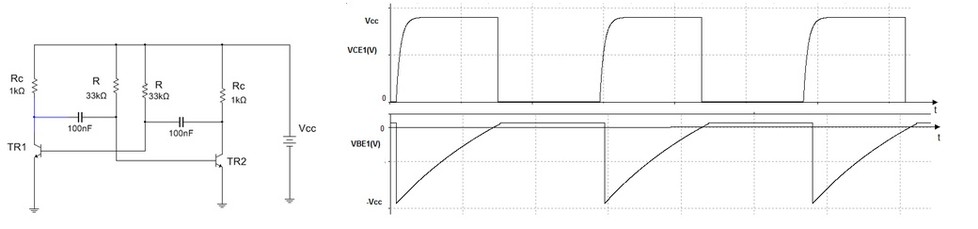
Figura 6 - Astavel simetrico (a ) Circuito ( b ) Formas de onda VCE1(t) e VBE1(t)
O Tempo de subida nos coletores pode ser zerado se forem adicionador o diodo D1 e a resistencia Rrec1, Figura 7a. Como não existe o D2 e Rrec2 no coletor 2 a tensão demora para atingir Vcc. Alem disso o circuito não é simetrico (semiperiodos diferentes).
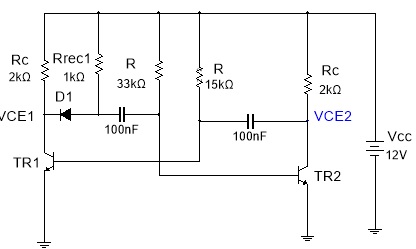
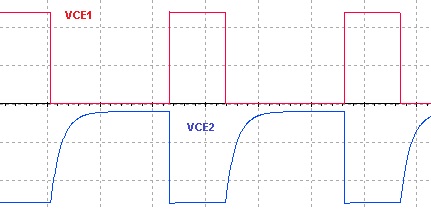
Figura 7 - ( a ) Astavel com tempo de subida 0 ( b ) Formas de onda nos coletores para circuito da Figura 7a
3. Exercício Resolvido
1.Projetar circuito astável simétrico que oscile na frequência de 200 Hz. Dados:
VC=12V ICsat = 6 mA bmin = 100. Calcular R, RC e C.
R =100 k e como T = 1/200Hz = 5 ms e T = 1,38.R.C obtemos :
C = 5.10-3/1,38.100.103= 3,6.10-8F =36 nF
4. Astavel como sinalizador (Pisca Pisca)
Caso seja colocado nos coletores LEDs, os mesmos podem acender e apagar com uma determinada frequencia visivel. No lugar de LED pode ser colocado relé que ligue uma lampada mais potente, Figura 8. O tempo que o LED fica aceso é dado por T=0,69.R.C
5. Experiencia: Astavel como sinalizador
5.1. Abra o arquivo ExpEN2_08 Astavel como Pisca Pisca (Multisim 14) e identifique o circuito da Figura 8.
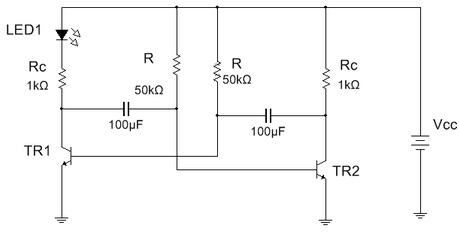
Figura 8 - Astavel como pisca pisca (Sinalizador)
Arquivo Multisim On Line - Sinalizador com Astavel
6. Experiencia: ExpEN2_09 Astavel Simetrico
6.1. Abra o arquivo ExpEN2_09 Astavel simetrico (Multisim 14), e identifique o circuito da Figura 9.
6.2. Calcule os tempo que o LED fica aceso e apagado, indicando na Tabela 1. Inicie a simulação e meça os tempos que o LED fica aceso e apagado incicando na Tabela 3.
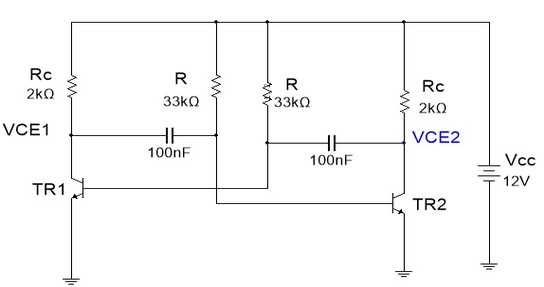
Tabela 1 - Valores calculados para o circuito da Figura 8.
Tempos Calculados | |||
TH(ms) | TL(ms) | T(ms) | f (Hz) |
6.3 Inicie a simulação e meça os tempos do item 6.2 Anote na tabela 2.
Tabela 2 - valores medidos para circuito da Figura 9
Tempos medidos por simulação | |||
TH(ms) | TL(ms) | T(ms) | f (Hz) |
6.4 Conclusões
7 Experiência: Astável com tempo de subida rápido
7.1 Abra o arquivo ExpEN2_10 Astavel com tempo de subida rapido (Multisim 14), e identifique o circuito da Figura 10a. Inicie a simulação e verifique as formas de onda nos coletores medindo os tempos.
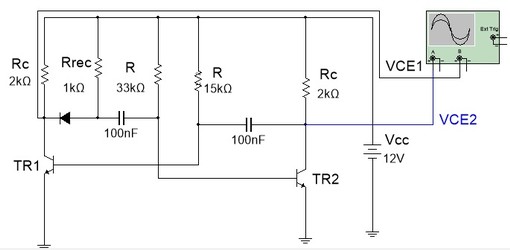
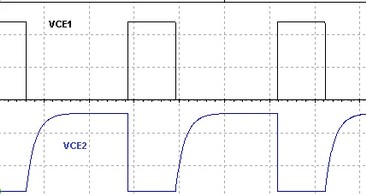
( a ) ( b )
Figura 10 - Astável com tempo de subida rápido no coletor ( a ) Circuito ( b ) Formas de onda nos dois coletores
Tempos Calculados | |||
TH(ms) | TL(ms) | T(ms) | f (Hz) |
7.3 Inicie a simulação e meça os tempos do item 7.2. Anote na tabela 4
Tabela 4 - Valores medidos para circuito da figura 10a
Tempos medidos por simulação | |||
TH(ms) | TL(ms) | T(ms) | f (Hz) |
7.4 Conclusões
