capacitorinicialmentecarregado - eletronica24h
Menu principal:
capacitorinicialmentecarregado
Educacional > Cursos > Eletricidade em CA
Carga do capacitor inicialmente carregado
Um capacitor carregado é equivalente a um capacitor descarregado em serie com uma bateria com o valor da tensão no capacitor.
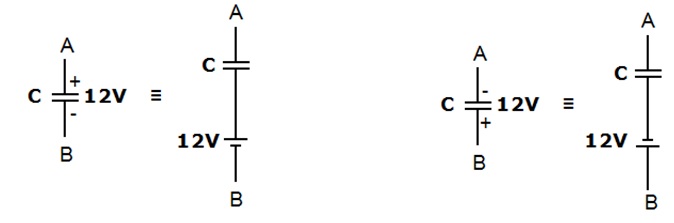
Figura 1 - Circuito equivalente para capacitor inicialmente carregado
Exemplo: Um capacitorestá inicialmente carregado com uma tensão de 12 V com a polaridade indicada na Figura 2. A chave CH é ligada no instante t=0. Pede-se:
a) Obter a expressão de Vc(t)
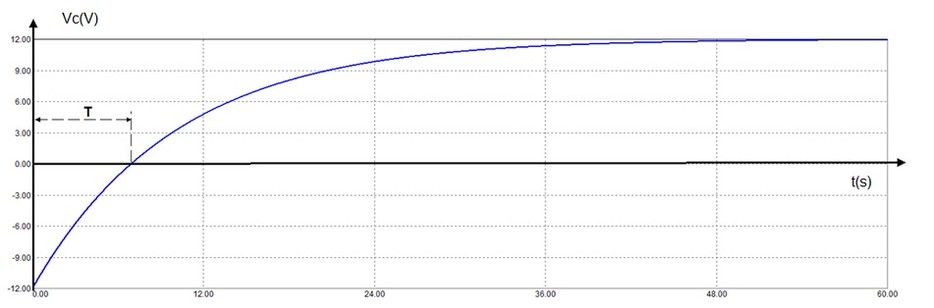
b) Calcular o tempo para a tensão em C atingir 0 V.
b) Calcular o tempo para a tensão em C atingir 0 V.
c) Desenhar o gráfico de vc9t)
Solução:
a) Considere o circuito com as condições impostas inicialmente
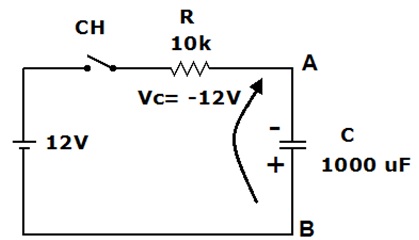
Figura 2 - Circuito exemplo
O capacitor carregado é equivalente a um capacitor descarregado em serie com uma bateria com polaridade e valor adequado. Seja Vc(t) a tensão no capacitor carregado (tensão entre os pontos A e B) e Vc’ (t) a tensão no capacitor descarregado (circuito equivalente) tensão entre os pontos A e X na Figura 3.
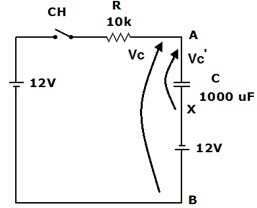
Figura 3 - Circuito exemplo, substituindo o capacitor carregado por um capacitor descarregado em serie com uma bateria
Redesenhando o circuito, considerando que as duas baterias estão em serie.
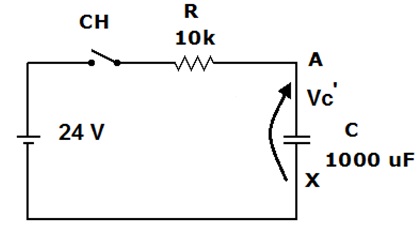
Figura 4 - Simplificando o circuito original
Temos um circuito conhecido, capacitor inicialmente descarregado onde a Expressão da tensão em função do tempo é conhecida. Qual a relação entre Vc(t) e Vc’ (t)? Voltando no circuito da Figura 3, obtem-se, por Kirchhoff:
Vc’(t) = Vc (t) +12
Vc’(t)=24.(1-e-t/R.C)
Portanto:
VC(t) = 24.(1-e-t/R.C) - 12
b) Para obter o tempo para que Vc=0, T, basta impor esse valor na expressão de vc(t).
VC(T)=0 = 24.(1-e-T/R.C) - 12 que resolvendo resulta:
Resolvendo obtém-se T=0,69.R.C=0,69.10k.1000 mF=6,9 s
Para verificar, calcule a tensão em t=0 e t= infinito para comparar com valores esperados. O gráfico de Vc(t) é:
c) Gráfico resultante. Veja a simulação
Arquivo Multisim Live
Figura 5 - Grafico da tensão no capacitor com uma carga imicial