Exercicios - eletronica24h
Menu principal:
Exercicios
Educacional > Cursos > Eletricidade em CA
zza
Exercicios propostos
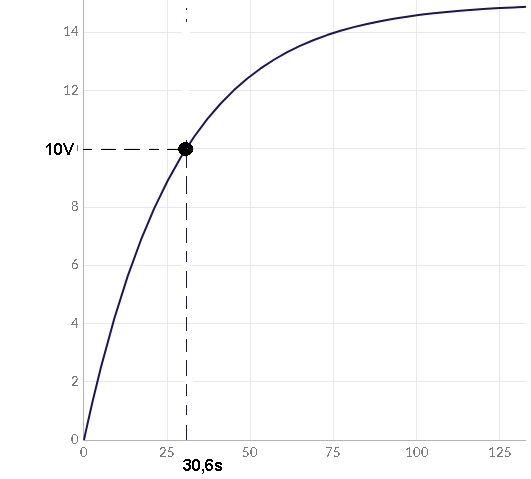
1) Dada a curva de carga de um capacitor de um circuito RC serie, pede-se determinar, usando o grafico:
a ) valor de C se R=56 k
b) valor da constante de tempo se a alimentação é de 15 V
c) Qual o tempo para Vc atingir 8V?
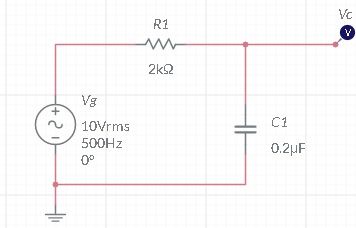
2) Dado o circuito RC serie com R1=2 k e C1=0,2mF. Determinar a tensão em Vc para as frequencias: 200Hz, 500Hz, 1kHz, 5kHz, 10kHz
3) Refaça o exercicio 2 considerando que o circuito é um FPB e portanto pode ser usada a expressão do ganho em função da frequencia da aula10 do curso CA
4) Dado o circuito determinar:
a) Impedância ( Z ) complexa nas formas polar e cartesiana
b) Corrente complexa na forma polar
c) Ângulo de defasagem entre a corrente total e a tensão total (f)
d) Potência aparente (S ou Pap) ativa (P) e reativa (Q ou Pr).
e) Desenhar o Diagrama fasorial
5) Um circuito consome 50 A quando ligado em 220 V, com um FP de 0,7. Determinar:
a) Qual a potencia ativa
b) Potencia aparente
c) Potencia reativa
d) Calcular o valor do capacitor que aumenta o FP para 0,92.
6) Um circuito RLC serie que tem R=50 Ohms, L=10 mH C= 10 nF é ligado em uma fonte de 10 V. Calcular:
a) Intensidade da corrente na ressonância
b) Impedância na ressonância.
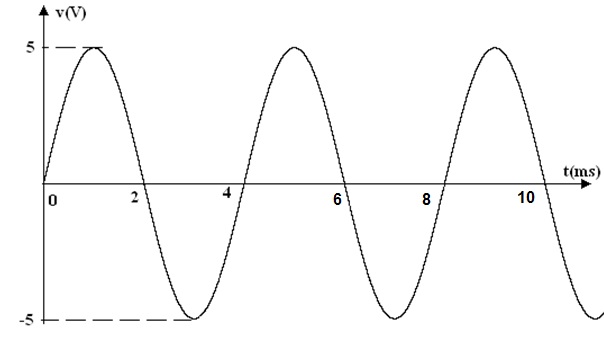
7) Dado a forma de onda de uma tensão pedem-se:
a) período (T)
b) freqüência (f)
c) expressão de v(t)
d) Valor de pico a pico (Vpp)
e) Valor eficaz (VRMS)
f) Potencia dissipada em uma resistencia de 5 ohms se v(t) for aplicada na mesma.
8) A tensão da questão 7 é aplicada a um resistor de 10 Ohms, pedem-se: a) Intensidade da corrente b) expressão da corrente em função do tempo c) Potencia dissipada.
9) Dado o diagrama fasorial com duas tensões, V1 e V2, pede-se:
a) Dar as expressões em função do tempo
b) Desenhar os gráficos das tensões em função do tempo sabendo-se que as suas freqüência são iguais a 100 Hz.
Obs : os valores são eficazes
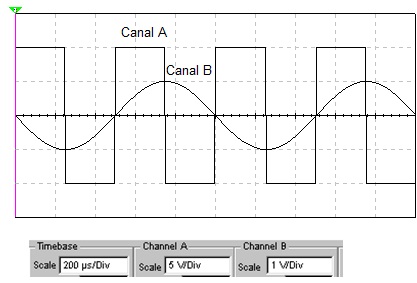
10) A figura mostra a tela de um osciloscopio com duas formas de onda, uma, quadrada, no canal A e outra, senoidal, no canal B. Os ajustes da base de tempo (tempo/Div.) e do ganho (Volts/Div.) são dados. Determinar o periodo, frequencia e o valor de pico a pico das duas tensões.
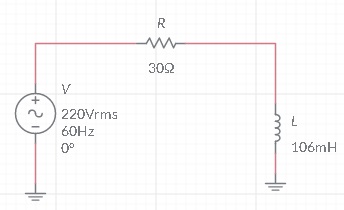
11) (Do livro Analise de Circuitos em CA ) Uma bobina quando ligada a uma fonte CC de 10 V consome 100 mA e quando ligada a uma fonte CA de 10 V/500 Hz consome 200 mA. Calcular:
a) Resistencia da bobina
b) Reatancia e indutancia da bobina
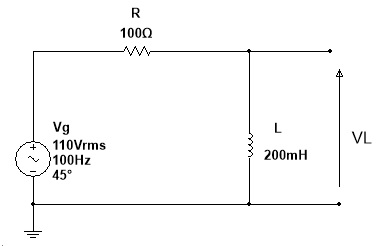
c) Impedancia complexa na foma polar
12) (Do livro Analise de Circuitos em CA pg82 ) Dado o circuito obter a tensão na resistencia, VR, e indutancia, VL, usando a expressão do divisor de tensão.
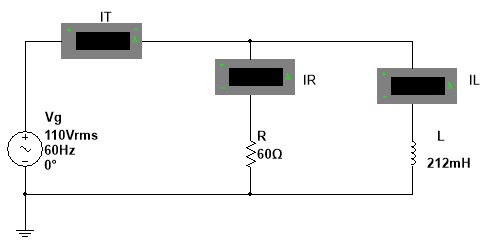
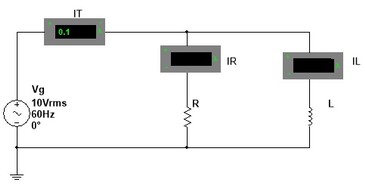
13) (Do livro Analise de Circuitos em CA pg 92 ) Dado o circuito, determinar:
a) Impedancia na forma cartesiana e polar
b) Valor das correntes na resistencia (IR) e indutancia (IL)
c) Fator de potencia do circuito (cosf)
d) Expressão da corrente TOTAL em função do tempo, i(t)
e) Desenhar o diagrama fasorial
14) (Do livro Analise de Circuitos em CA pg 99 ) Uma instalação consome 5 kW. Sabend-se que a potencia reativa é de 3 kVARi e que a tensão é 220 V calcular:
a) Fator de potencia
b) Corrente consumida
c) Valor de R
15) (Do livro Analise de Circuitos em CA pg 99 ) Em um circuit RL paralelo, a defasagem entre a tensão e a corrente é de 30 graus. Sabendo-se que a tensão e a corrente consumidas valem respectivamente 10 V e 100 mA e que a fase da tensão é 0 graus de frequencia 60 Hz, calcular:
a) Expressão de i(t) e iL(t)
b) Impedancia nas formas cartesiana e polar
c) Desenhar o Diagrama Fasorial
16) Dado as duas tensões:
v1(t)=15.sen(2000.p.t + 300)(V) e
v1(t)=15.sen(2000.p.t + 300)(V) e
v2(t)=15.sen(2000.p.t + 600)(V),
Determinar:
a) frequência das duas tensões
a) frequência das duas tensões
b) Valor da duas tensões no instante t=0.
c) Obter v3(t)=v1(t)+v2(t) nas formas polar, cartesiana e em função do tempo