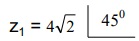NumerosComplexos - eletronica24h
Menu principal:
NumerosComplexos
Educacional > Cursos > Eletricidade em CA
Números Complexos
Os Numeros complexos são ferramentas poderosas na resolução de circuitos em corrente alternada, por isso a necessidade dos mesmos terem essa aula.
Voce sabe qual o resultado dessa operação?
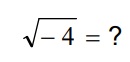
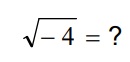
No conjunto dos numeros reais não tem solução, mas no conjunto dos numeros complexos tem!
Definição: Unidade imaginaria
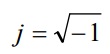
ou
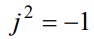
Desta forma:
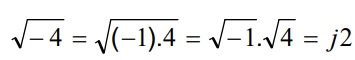
O seu professor de matematica pode usar a letra i ao inves de j.
Deduções:
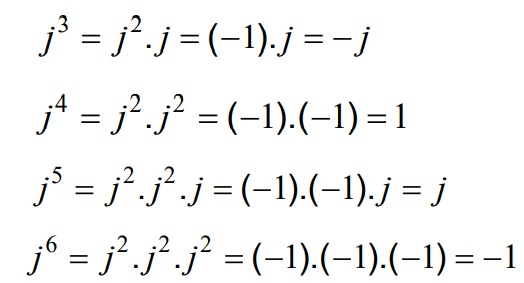
Exemplos: Z1=5+j8 Z2=j20 Z3= 15 Z4= -50-j20
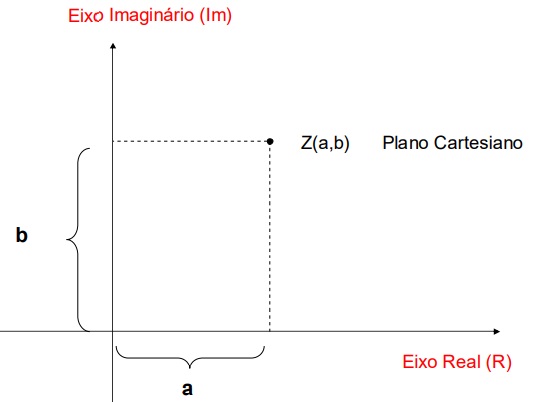

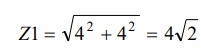
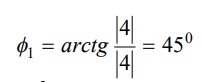
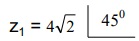
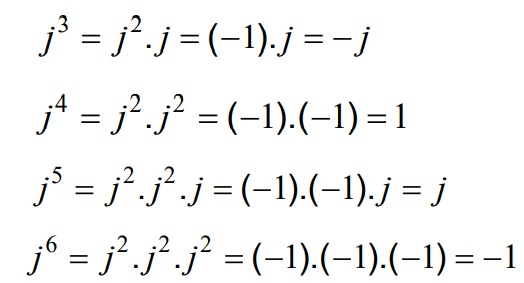
Formas de representar um numero complexo
- Forma cartesiana;
- Forma Polar;
- Forma Trigonometrica.
A forma Cartesiana ou Retangular
Z=a+jb onde a e b são numeros reais e j é a unidade imaginaria ( em matematica é usado a letra i, em eletricidade para não confundir com intensidade de corrente é usado o j).
Exemplos: Z1=5+j8 Z2=j20 Z3= 15 Z4= -50-j20
È assim chamada pois é representada no plano cartesiano.

Exemplos: Representar os numeros no plano cartesiano:
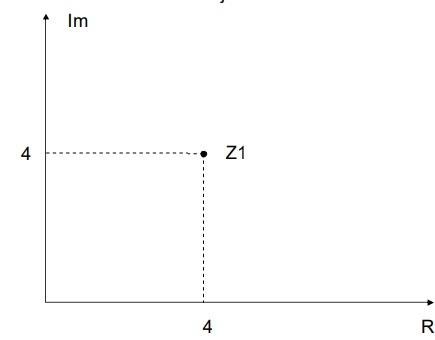
Z1=4 + j4
Z1=4 + j4

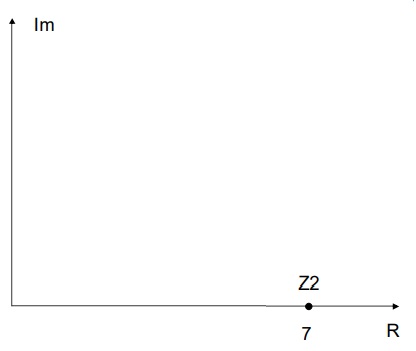
Z2=7 (não tem parte imaginária)

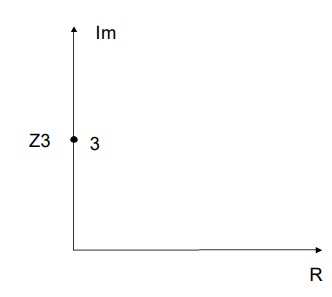
Z3=j3 (não tem parte real)

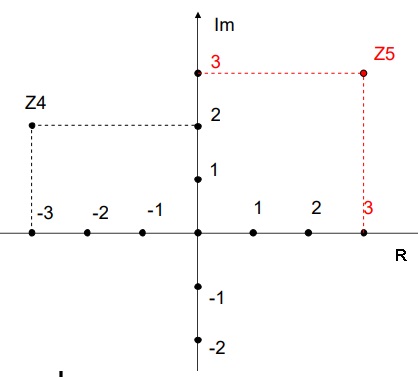
Z4=-3+j2 e Z5=3+j3

A Forma Polar
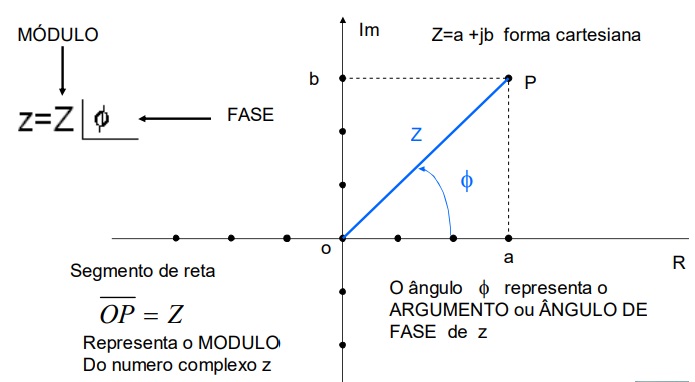
A forma polar mostra o modulo e a fase.

Na forma polar um numero complexo é representado por:

Numero complexo é representado por letra minúscula, z, e o seu modulo por letra maiúscula, Z.
Existe uma forma onde um ponto em cima indica que a grandeza é vetorial
Transformação da forma Cartesiana para Polar
Na analise de circuito em CA, as operações requerem que saibamos transformar de uma forma para outra.
É dada a forma cartesiana Z=a+jb e deve ser obtido o modulo e a fase do numero complexo, forma Polar.
Procedimento: Indique no plano cartesiano Z=a+jb
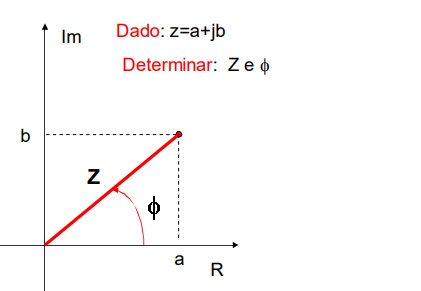

O modulo de Z é obtido usando teorema de Pitagoras
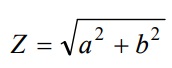
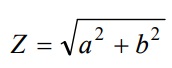
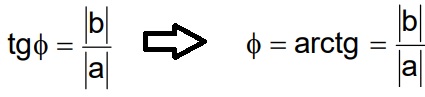
O angulo de fase f, é obtido do triangulo retangulo.

Exemplo: Dado o numero complexo na forma cartesiana Z1=4+j4, obter a forma polar
Solução
1) Representar o numero no plano cartesiano
: 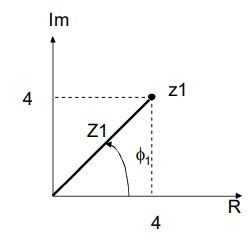

2) Usando pitagoras obter o modulo do nuero complexo
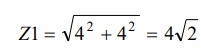
3) Determinar o angulo f1
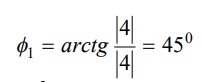
3) Excrever Z1 na forma polar