aulaCA001 - eletronica24h
Menu principal:
aulaCA001
Educacional > Cursos > Eletricidade em CA
Analise de Circuitos em Corrente Alternada
Aula01: Tensão Alternada - Tensão Senoidal - Circuito Resistivo em CA
Bibliografia
Analise de Circuitos em Corrente Alternada - Editora Erica
1 Tensão Continua
Como você bem sabe, uma tensão é chamada de continua ou constante pois o seu valor não se altera com o tempo. Exemplo de geradores que geram tensão continua são as pilhas e as baterias. A Figura 1 mostra o aspecto físico, símbolo e curva da tensão em função do tempo deste tipo de gerador.
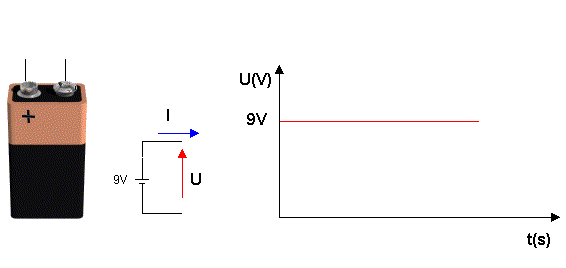
( a ) ( b ) ( c )
Figura 1: Gerador de tensão continua - ( a ) Aspecto físico ( b ) Símbolo e ( c ) gráfico da tensão em função do tempo
O gráfico da figura 1 mostra o comportamento da tensão nos terminais da bateria ao longo do tempo: A tensão não muda, permanece constante.
2 Tensão Alternada
É uma tensão cujo valor e polaridade se modificam ao longo do tempo. Conforme o comportamento da tensão então temos os diferentes tipos de tensão: Senoidal, quadrada, triangular, pulsante, etc.
De todas essas, a senoidal é a que tem um maior interesse pois é a tensão que é gerada nas usinas e que alimenta as industrias e residências. Antes de estudarmos mais a fundo a tensão senoidal, vamos procurar conceituar melhor a tensão alternada. Seja o circuito da Figura 2, no qual temos duas baterias e uma chave que ora conecta a bateria B1 ao resistor, ora conecta a bateria B2 ao resistor. Vamos supor que cada bateria fica conectada ao resistor durante 1s. Como seria o gráfico da tensão em função do tempo nos terminais da bateria ?
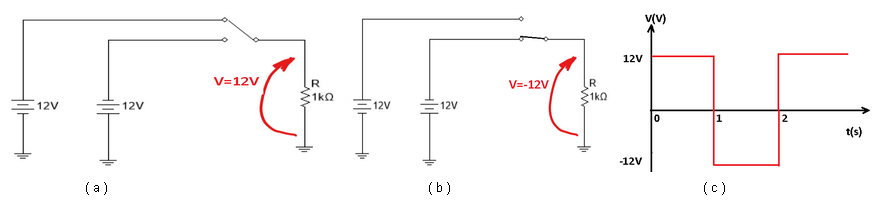
Figura 2 - Gerando uma tensão alternada quadrada - ( a ) Circuito com V=12V ( b ) Circuito com V=-12V ( c ) Tensão em função do tempo
Observe que:
O valor negativo significa que a polaridade da tensão mudou. O tempo que leva para repetir uma mesma situação é 2s, sendo chamado de período (T). O valor máximo da tensão é 12 V (com qualquer polaridade, sendo chamado de valor de pico ou valor máximo VM). A seguir estudaremos mais em detalhes a tensão senoidal.
A animação ajuda voce a entender uma tensão quadrada.
Figura 3 - Animação mostrando um voltimetro medindo uma tensão quadrada
3.1 Tensão senoidal
A tensão mais comum, e mais facil de ser gerada, é a tensão senoidal. É a tensão fornecida para alimentar as industrias e a sua casa.
É uma tensão que varia com o tempo de acordo com uma lei senoidal, portanto nesse caso temos uma expressão matemática para expressar a tensão. A expressão matemática é:
v(t)=VM.sen(w.t+qo)
ou em função do angulo
v(q)=VM.sen(q)
Onde VM (em V), ou Vp, é o valor de pico (valor maximo que a tensão pode ter) e w(ômega) em (rd/s) é a freqüência angular
q0 em (rd ou graus) é o angulo de fase inicial, q (teta) é o ângulo num determinado instante t.
Observe que a relação entre ângulo e tempo é dada por:
q= q0 + w.t
Esta equação é análoga à equação que rege o movimento uniforme de um móvel:
S= S0+ v.t onde S0 é o espaço inicial em relação à origem
3.1.1 Representação Grafica e matematica de uma tensão senoidal
A primeira forma de representar uma tensão senoidal é a forma grafica e a segunda forma é a expressão matematica.
Uma tensão senoidal varia em função do tempo de acordo com uma lei senoidal, portanto a sua representação será como na Figura 4a, mas a mesma tensão pode ser representada em função do angulo, Figura 4b, (não esqueça que a função seno tem período de 360 graus ou de 2p rd), sendo a relação entre angulo e tempo dada por :
q=q0 + w.t
onde
qo (teta zero) é o angulo de fase inicial, w é afrequencia angular (em rd/s) e t é o tempo em s.
A Figura 4 mostra o gráfico da tensão em função do tempo cuja expressão matematica é:
v(t)=10.sen(w.t) nesse caso o angulo de fase inicial é zero.
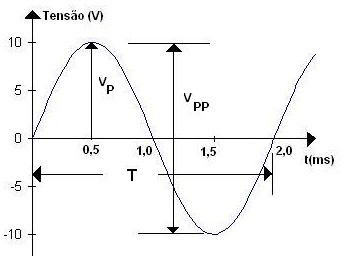
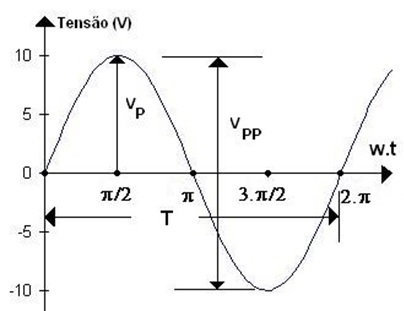
( a ) ( b )
Figura 4 - Representação gráfica de uma tensão senoidal (a ) em função do tempo ( b ) em função do angulo
Na Figura 4a e Figura 4b, VPP (em V) é chamado de tensão de pico a pico, T (em s) é o período (tempo que o fenômeno leva para se repetir). Observe que o periodo no exemplo da Figura 4 pode ser expresso no tempo ou em angulo, isto é: T=2 ms ou T= 2.p rad
Pelos gráficos da Figura 4a e Figura 4b tiramos as seguintes conclusões:
como q=w.t se q =2.p >>>>> t=T logo substituindo em q=w.t resulta:
2.p=w.T ou w = 2.p/T
O numero de ciclos completados segundos chamamos de freqüência (f). A freqüência está relacionada com o periodo por:
f =1/T (Hz) logo pode-se escrever que:
w=2 .p.f
Por exemplo se f=60 Hz w=2 .p.60=377 rd/s
Expressão muito importante que mostra a relação entre frequencia angular dada em rd/s e frequencia dada em Hz ou ciclo/s
Em relação à tensão mostrada na Figura 4: Vp=10V Vpp=20V T=2ms a frequencia f=1/T=1/2ms= 500 Hz w=2 .p.500= 1000.p=3.140 rd/s
__________________________________________________________________________________________________________________

Como é exatamente a variação da tensão senoidal? Seja uma tensão alternada senoidal de 10V de pico e frequencia 60Hz.
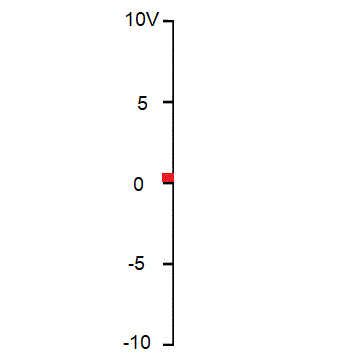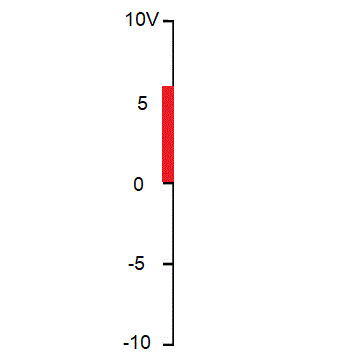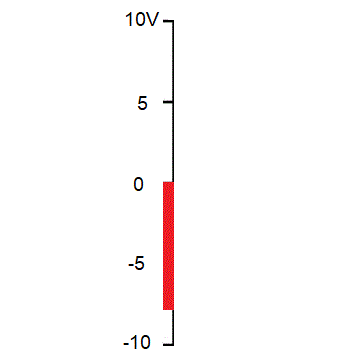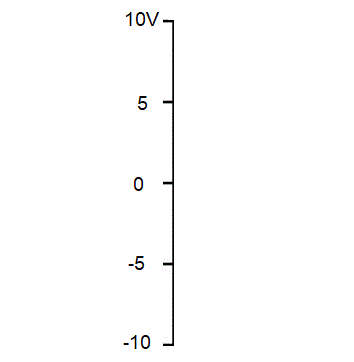
A subida e a descida segue uma lei senoidal. Na tomada é igualzinho, a diferença é que o valor de pico é 156V.
_______________________________________________________________________________________________________________
3.1.2 Tensão eficaz
Para uma tensão senoidal definimos o seu valor eficaz (VRMS ou VEF) como sendo igual ao valor de uma tensão contínua que produzirá a mesma dissipação de potência que a tensão alternada em questão. No caso de uma tensão senoidal o seu valor eficaz é calculado por:
Definição matemática:
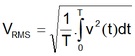
Para o caso particular de uma tensão senoidal o valor é dado por:
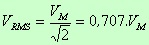
Obs:
- considerar raiz de 2 como sendo aproximadamente igual 1,41 para efeitos de calculos;
- RMS= Root Mean Square = valor quadrático médio.
Para exemplificar: Se uma tensão senoidal de 110V (eficaz) for aplicada a uma resistencia de 11 Ohms, a dissipação de potencia , portanto o calor gerado, será o mesmo que se uma tensão CC de 110V fosse aplicada a mesma resistencia . Esse é o significador de valor eficaz.
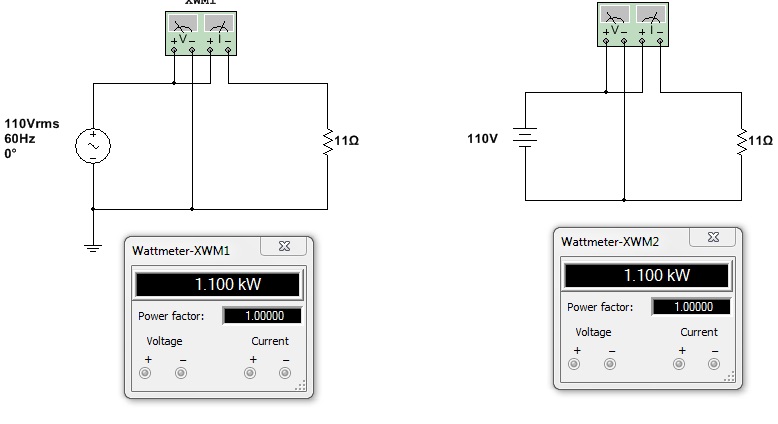
Figura 5 - ( a ) Tensão senoidal de valor eficaz 110 V (155 V de pico) aplicada a um resistor de 11 Ohms; ( b ) Tensão continua de valor igual ao valor eficaz da tensão senoidal aplicada a um resistor de 11 Ohms
Para a tensão senoidal representada na Figura 5 os seus parâmetros são: VP=VM=110. 1,41=155 Vpico VPP =310 Vpp
VRMS =155/1,41=110 V
VRMS =155/1,41=110 V
T=0,01666s=16,66 ms portanto f= 1/0,0166 = 60 ciclos/s = 60 Hz
w=2.p.60=377 rd/s qo=0
Um resistor de 11 Ohms ao ser conectado a essa tensão senoidal, dissipará a mesma potência se for conectado a uma tensão CC de 110 V
Outro exemplo para voce entender valor eficaz.
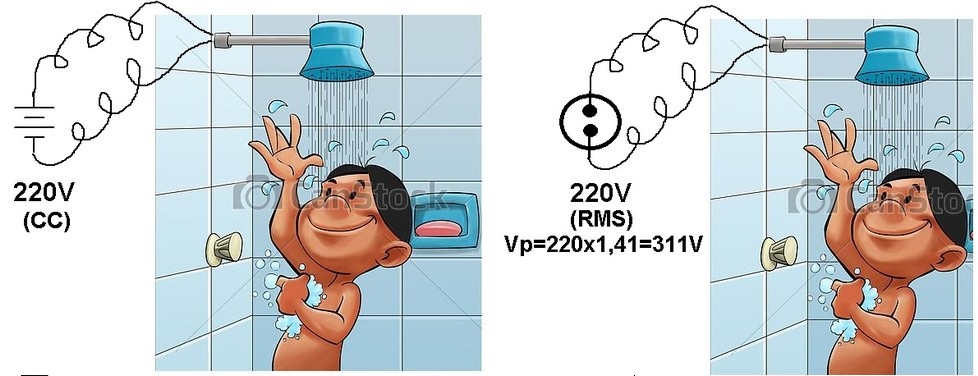
O chuveiro da sua casa é ligado a uma tensão alternada de 220V eficazes, que corresponde a uma tensão de pico de aproximadamente 311V. Se voce dispuser de uma bateria de 220V (CC) com capacidade de corrente suficiente, pode ligar o chuveiro que o aquecimento será o mesmo.
PS: Nos EUA não é usado o chuveiro com resistencia para o banho, a agua é aquecida com gás ou oleo.
PS: Nos EUA não é usado o chuveiro com resistencia para o banho, a agua é aquecida com gás ou oleo.
Exercício1:
Representar as seguintes tensões senoidais no grafico em função do tempo Qual a frequencia e a frequencia angular em cada caso? Qual o valor eficaz em cada caso?
v1(t) = 15.sen(2.p.103.t ) ( V ).
v2(t) = 20.sen(2.p.103.t + p/2 )( V ).
Arquivo Multisim Live
Da expressão de v1 obtemos que a frequencia angular w=2.p.103 rd/s e portanto como w=2.p.f
f1=1000 Hz=1 kHz, e T1=1ms=0,001 s.
O valor de pico desta tensão, V1, é VM =15 V, angulo de fase inicial qo=0º
O seu valor eficaz
VRMS1 =15/1,41=10,6 V
Da mesma forma para v2: w=2.p.103 rd/s e portanto
f2=1000 Hz=1 kHz, e T2=1 ms=0,001 s
o valor de pico desta tensão é 20 V, angulo de fase inicial qo=90º=p/2.
O valor eficaz VRMS2 =20/1,41=14,2V
A seguir os gráficos das duas tensões
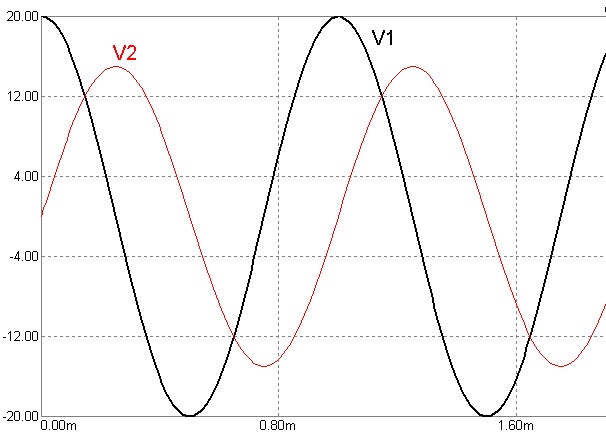
Exercício Resolvido 2:
V1(t)=5.sen(104p.t + 90o)(V) e V2(t)= 5.sen(104p.t - 90o)(V)
Arquivo multisim Live
Os dois sinais tem a mesma frequência angular ω= 104.p rd/s
E como ω= 104.p rd/s então f= 104p/2.p =5000 Hz=5 kHz
O valor eficaz das duas tensões é o mesmo VRMS1 =5/1,41=3,54 V = VRMS2
O ângulo de fase inicial da tensão V1 é qo=90o e da tensão V2 é qo= - 90o
Exercício Resolvido 3:
Representar as seguintes tensões senoidais
V1(t)=155.sen(120.p.t - 450)(V) e V2(t)= 155.sen(120.p.t)(V)
Arquivo Multisim Live
Solução:
O valor de pico das duas tensões é o mesmo Vp1=Vp2=155 V e da mesma forma o valor eficaz VRMS1=VRMS2=155V/ 1,41=110V
O angulo de fase inicial da tensão V1 é qo=-450
O angulo de fase inicial da tensão V2 é zero, qo=0
A seguir o Diagrama Fasorial e os gráficos da tensão em função do tempo, sendo que o gráfico em violeta representa V1 e V2 em preto
Obs: O Diagrama Fasorial é outra forma de representar uma tensão senoidal
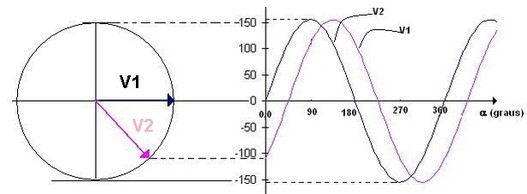
Figura 6 - Diagrama fasorial e tensões do exercicio 3
3.1.3 Diagrama Fasorial
O Diagrama Fasorial (D.F) é terceira forma de representar uma tensão senoidal. O D.F é representado por um fasor (vetor girante) que gira com frequencia angular w no sentido anti horario. O fasor representativo da tensão é indicado sempre no instante t=o.
A Figura 7 mostra como é construído o diagrama fasorial. Cada vetor (neste caso chamado de fasor), representa a tensão num determinado instante. Observe que o ângulo que o fasor faz com o eixo horizontal representa o ângulo da tensão naquele instante.
No exemplo da figura 7b a tensão representada tem a expressão: v(t)=10.sen(w.t) (V)
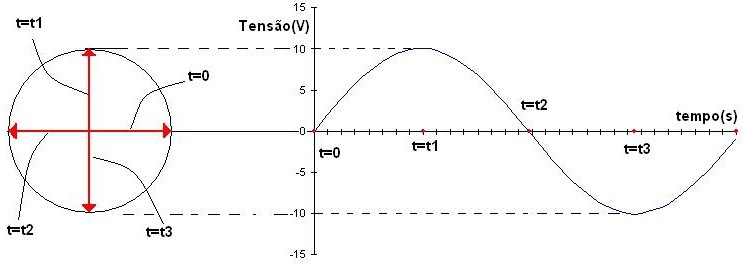
( a ) ( b )
Figura 7 - ( a ) Diagrama fasorial ( b ) Forma de onda correspondente
Dê uma olhada nessa animação que mostra o Movimento Circular Uniforme (MCU)
O diagrama da Figura 7a representa a tensão da Figura 7b que no instante t=0 vale zero e portanto a expressão da tensão em função do tempo é:
v(t) =VM.sen(w.t) pois qo (angulo de inicial) vale zero. Caso a tensão tivesse um angulo inicial, a expressão seria dada por:
v(t) =VM.sen(w.t+qo) se a tensão estiver adiantada ou
v(t) =VM.sen(w.t - qo) se atrasada.
A animação a seguir ajudará voce a entender o Diagrama Fasorial. Observe que a projeção no eixo vertical do fasor representa a tensão naquele instante.
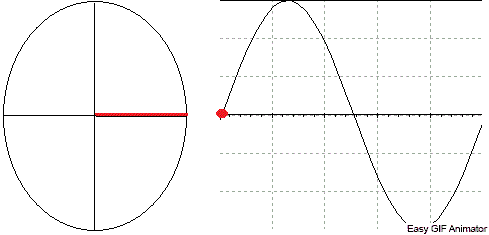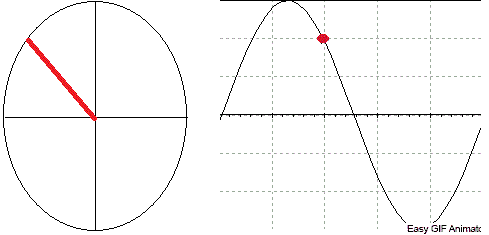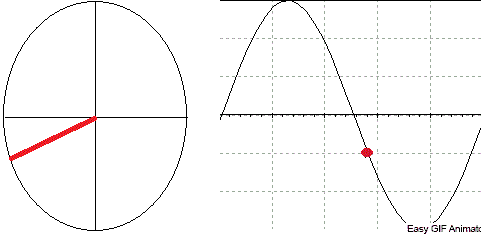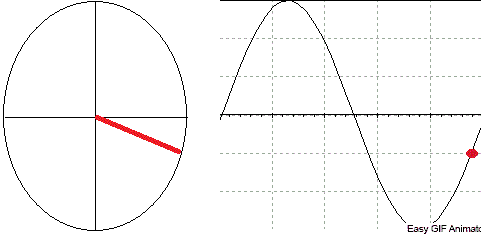
_______________________________________________________________________________________________________________
3.4 Angulo de fase inicial
Como visto, uma tensão pode ser representada matematicamente por:
v(t)=10.sen(w.t + q0 ) onde qo é o angulo de fase inicial .
Se no instante t=0 a tensão for zero o sinal parte da origem logo qo=0 . Se no instante t=0 o valor da tensão for positiva dizemos que o sinal esta adiantado em relação a origem e se no instante t=0 a tensão for negativa o sinal esta atrasado.
SINAL ADIANTADO (Em relação a origem de angulo)
Um sinal (tensão ou corrente) está adiantado em relação a origem, se já passou pela origem, Fgura 8. Não esqueça a orientação de angulo é no sentido anti horario.
Ex: v(t)=10.sen(w.t + 900) O valor de pico é 10 V e o angulo de fase inicial (teta zero)=900
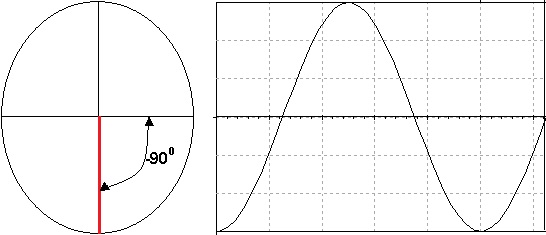
Figura 8 - Diagrama fasorial e forma de onda da tensão v(t)=10.sen(w.t + 90º)(V) - sinal adiantado
SINAL ATRASADO (Em relação a origem de angulo) - SINAL NA ORIGEM
Um sinal (tensão ou corrente) está atrasado em relação a origem, se ainda vai passar pela origem, Fgura 9a.
Ex: v(t)=10.sen(w.t - 900 ) angulo de fase inicial= - 900 ou 2700
Quando um sinal (tensão ou corrente) está na origem, dizemos que o angulo de fase inicial é zero, Fgura 9b.
Ex:
v(t)=10.sen(w.t )(V)
Sinal Atrasado
Arquivo Multisim - Sinal atrasado
Sinal na origem
Arquivo Multisim - Sinal na origem
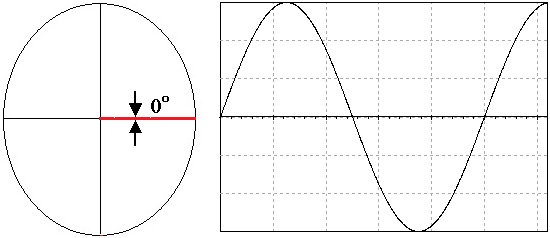
Figura 9 - ( a ) Diagrama fasorial e forma de onda da tensão v(t)=10.sen(w.t - 90º)(V) ( b ) Diagrama fasorial e forma de onda da tensão v(t)=10.sen(w.t)(V)
______________________________________________________________________________________________________________
3.1.4 Representação na forma complexa de uma tensão senoidal
Sabemos que um numero complexo tem modulo e fase, e como uma tensão tambem tem modulo e fase então uma tensão alternada senoidal tambem pode ser representada na forma complexa, isto é:
Forma Trigonometrica:
Exemplo1: Seja a atensão V(t)=100.sen(ω.t + 600)(V) O valor de pico é 100 V e o ângulo de fase inicial é qo=600
Formas Complexas:
Como uma tensão (corrente) tem modulo e fase, podem ser representadas nas formas complexas cartesiana e polar.
Forma polar
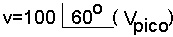
Forma Cartesiana
V=VM.cos q0 + jVMsen qo = 50 + j86,66 (Vpico)
Exemplo2: Seja a tensão V(t)=12.sen(w.t+600)(V)
Forma cartesiana: V=12.cos60 + 12.sen60 = 6 +j10,39 (V)
Forma polar:
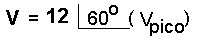
Forma polar: Usada para multiplicação e divisão Forma cartesiana: somar ou subtrair duas tensões
A analise de circuitos em CA pode ser feita usando o Diagrama Fasorial ou usando as fomas complexas. Em circuitos simples podem ser usadas as duas formas, mas em circuitos com muitos componentes a forma complexa é mais adequada.
4 Experiencia: Tensão alternada - Osciloscopio
4.1 O osciloscopio (O) é o instrumento que permite ver uma tensão alternada, nesta experiencia voce aprenderá a medir os valores de de tensão e tempo usando o osciloscopio. As tensões alternadas são obtidas no gerador de funções (GF). Ambos são obtidos na barra de instrumentos à direita (Multisim).
4.2 Abra o arquivo ExpCA01_tensão_alternada_osciloscopio_GF (Multisim 14) e nnicie a simulação. Abra o osciloscopio e veja as formas de onda senoidal, triangular e quadrada (para ver esta voce deve colocar a chave na outra posição).
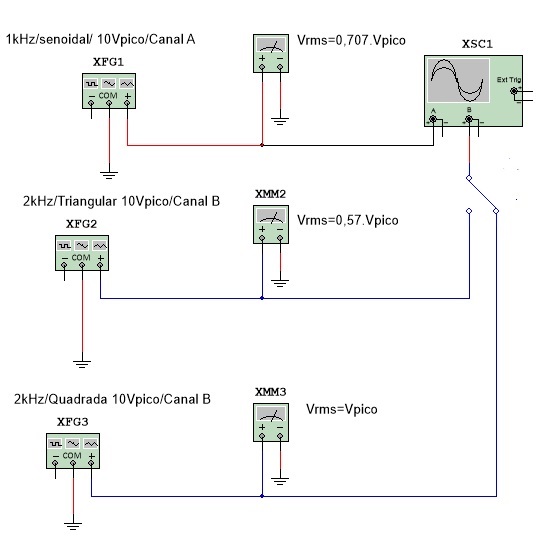
Figura 10 - O gerador de Funções e o Osciloscopio
Clique aqui para acessar o arquivo Multisim Live - Como obter tensão senoidal, tensão quadrada e tensão triangular
4.3 Para medir o valor de pico a pico, Vpp, com o osciloscopio, conte o numeros de divisões que o sinal ocupa na vertical e faça a conta. Vpp= Numero divisõesxVolts/Div.
Obs: Se voce estiver usando Multisim Live, use os dois cursores. Em Cursors>>Type Selecione YAxis. Aparecerão dois cursores na horizontal, C2 e C1. Escolha qual tensão deseja medir, por exemploV1.Posicione C2 no pico superior e C1 no pico inferior. Embaixo em DY será mostrado o valor de pico a pico. Eventual erro será por conta do posicionamento.
4.4 Para medir o valor do periodo, T, conte o numeros de divisões que o sinal ocupa na horzontal e faça a conta. Vpp= Numero divisõesxTime/Div.
4.5 Anote o valor de pico a pico, o valor eficaz de cada uma das 3 tensões (senoidal, triangular e quadrada).
Senoidal: Vpp=____________ VRMS=__________________ Periodo=_______________
Triangular: Vpp=____________ VRMS=__________________ Periodo=_______________
Quadrada: Vpp=____________ VRMS=__________________ Periodo=_______________
4.6 Experiemente mudar amplitude/frequencia.
4.7 Escreva as suas conclusões.
5. Experiencia: Angulo de fase inicial de uma tensão senoidal - Defasagem
5.1 Abra o arquivo ExpCA02_Angulo de fase inicial e defasagem (Multisim 14) e identifique o circuito da Figura 11.
5.2. Inicie a simulação em seguida abra o osciloscopio. Observe as duas formas de onda.
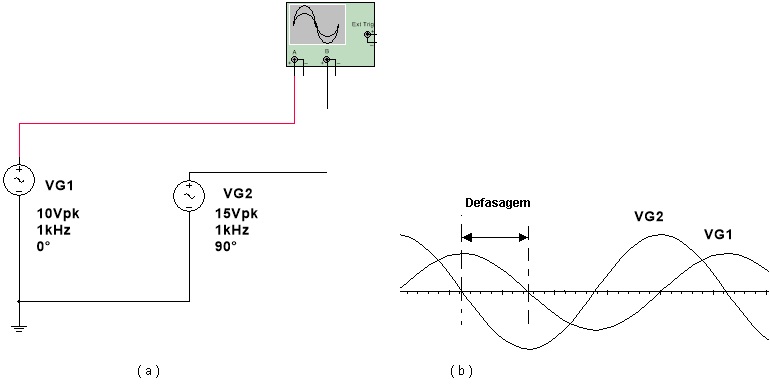
( a ) ( b )
Figura 11 - Medindo a defasagem entre duas tensões ( a ) circuito ( b ) formas de onda
Figura 11 - Medindo a defasagem entre duas tensões ( a ) circuito ( b ) formas de onda
5.3 Meça a defasagem no tempo usando os dois cursores do osciloscopio.
5.4 Usando proporcionalidade determine a defasagem em graus. Não esqueça que os sinais tem f=1 kHz T=1ms.
5.5 Compare com a defasagem especificada nos geradores.
5.6 Exprimente mudar o angulo de fase inicial das tensões para outros valores e depois repitaos itens anteriores.
5.7 Escreva as suas conclusões.
6 Somando Tensões Senoidais
A soma de tensões (ou correntes) segue a mesma regra para soma de numeros complexos. Consideremos um exemplo.
Exercicio Resolvido 4:
Sejam as tensões
v1(t) = 15.sen(2000.p.t ) ( V ) e v2(t) = 20.sen(2000.p.t + p/2 )( V ). Obter v3(t)=v1(t)+v2(t)
Solução:
Voce pode resolver graficamente representando as duas tensões no mesmo Diagrama Fasorial e efetuar a soma vetorial, Figura 12.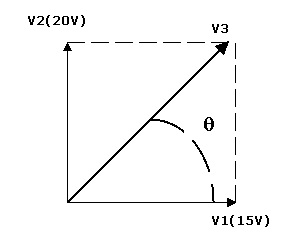
Figura 12 - Diagrama Fasorial de duas tensões senoidais
O modulo de v3 é calculado por:
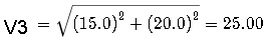
Onde o angulo de fase inicial pode ser calculado por:
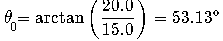
Poderia representar as duas tensões na forma cartesiana: V1=15+j0 (Vpk) V2=0 +j20(Vpk) e somar as duas obtendo V3=15+j20(Vpk) e esse numero complexo que representa a tensão soma tem modulo igual a 25Vpk e fase inicial = 53,13 graus, isto é
v3(t)=25.sen(2000.p.t+53,13)(V)
7 Experiencia: Soma de tensões senoidais
7.1 Abra o arquivo ExpCA03_Somando_duas_tensões_senoidais (Multisim 14) e identifique a Figura 13. Nesse circuito as duas tensões senoidais v1(t) e v2(t) são somadas para obter v3(t), isto é:
v3(t)=V1(t)+v2(t) onde v1(t)=20.sen(w.t+90)(V) e v2(t)=14.sen(w.t)(V)
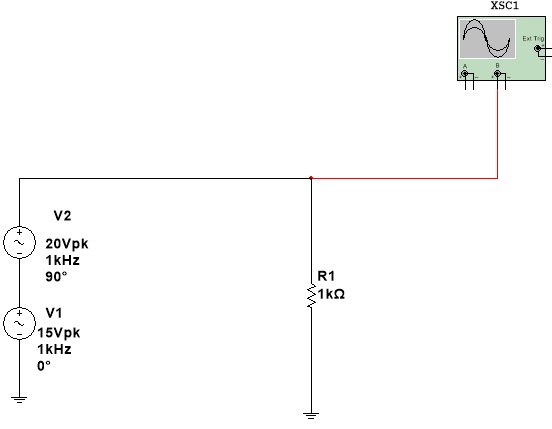
Figura 13 - Somando duas tensões senoidais
Clique para acessar o arquivo Multisim Live
7.2 Meça o valor de ´pico e o valor da tensão no instante t=0 da tensão soma, isto é v3(t). Com esses dois valores determine o angulo de fase inicial.
Vpk=__________ qo=________
v3(t)= Vpk.sen(w.t+qo) para t=0 v3(0)=Vpk.sen(qo) logo qo=arcsen(v3(0))/Vpk)
7.3. Experimente considerar outros valores de amplitude e angulos
7.4. Escreva as suas conclusões.
8 Exercicios Propostos
8.1 Para os sinais pedem-se determinar:
a) Freqüência angular
b) freqüência
a) Freqüência angular
b) freqüência
c) Periodo d) Ângulo de fase inicial e) Representar graficamente
f) Indicar o valor da tensão para t=0
v1(t)=10.sen(20.000. π.t + π/3) (V) V2 (t)=15.sen(8.000. π.t – 300) (V)
8.2 Desenhar o Diagrama Fasorial dos sinais
v1(t)=10.sen(w.t + 60) (V) v2(t)=15.sen(w.t - 30) (V)
8.3 Para os sinais pedem-se determinar:
v1(t)=10sen(w.t+π/3) (V) v2(t)=15.sen(w.t - π/6 ) (V)
a) Defasagem
b) Obter V3=v1+V2
b) Obter V3=v1+V2
c) representar v1 e v2 no D.F
c) Dar a expressão de V3(t)
d) Representar V3 na forma polar e cartesiana