aulaCA002 - eletronica24h
Menu principal:
aulaCA002
Educacional > Cursos > Eletricidade em CA
Analise de Circuitos em Corrente Alternada
Aula02: Circuitos Resistivos em CA
Bibliografia
Analise de Circuitos em Corrente Alternada - Editora Erica
Aula02: Circuitos Resistivos em CA
Bibliografia
Analise de Circuitos em Corrente Alternada - Editora Erica
1. Circuito puramente resistivo
Em um circuito puramente resistivo (só com resistências) alimentado com uma tensão alternada senoidal (CA) a tensão e a corrente estão em fase, sendo a relação entre elas dada pela lei de ohm, isto é :
V =R.I ou I = V/R onde V é a tensão, em Volts, aplicada na resu]istencia R, Ohms, e I é a intensidade da corrente em Amperes.
Em termos de diagrama fasorial significa que os fasores representativos da tensão e da corrente estão em fase. A Figura 1 mostra o diagrama fasorial da tensão e da corrente e o circuito.
Obs: Quem é maior a tensão ou a corrente? Não podemos comparar grandesas diferentes. Quem é maior 2 kg ou 10m? Entendeu?
Obs: Quem é maior a tensão ou a corrente? Não podemos comparar grandesas diferentes. Quem é maior 2 kg ou 10m? Entendeu?
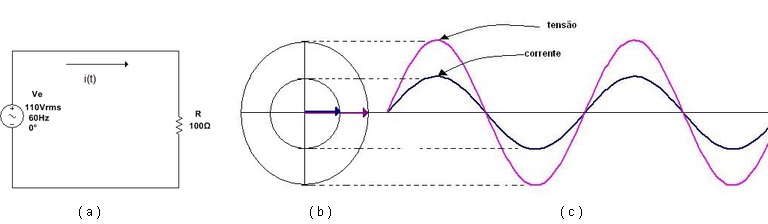
( a ) ( b ) ( c )
Figura 1 - ( a ) circuito puramente resistivo em CA ( b ) diagrama fasorial ( c ) formas de onda da corrente
Se a tensão é senoidal: v(t)=Vp.sen(w.t + q0)(V) Vp é o valor de pico da tensão, w é a frequencia angular em rd/s e q0 é o angulo de fase inicial (rd ou graus)
A corrente tambem será senoidal e em fase com a tensão podendo ser determinada usando a primeira lei de Ohm.
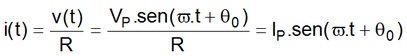
Ip é o valor de pico da corrente em amperes
O valor de pico da corrente pode assim ser determinado:
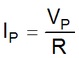
Como tensão e corrente estão em fase, concluímos que:
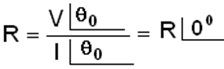
ou R= R + j0 formas polar e cartesiana
Uma resistência pode ser representada por um numero complexo com parte imaginaria nula.
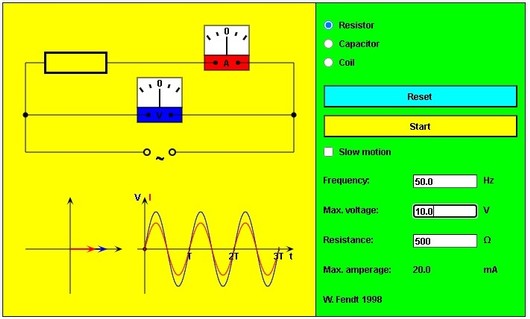
A seguir uma aplicação Java que mostra o Diagrama Fasorial e formas de onda de corrente e tensão em um circuito puramente Resistivo.
Selecione Resistor para ver o Diagrama Fasorial e formas de onda da tensão e corrente. Clique em Start
2. Potencia em CA
O calculo da potencia dissipada em uma resistencia é calculada da mesma forma que em CC somente que os valores de tensão e corrente são chamados de valores eficazes. O que valor eficaz?
Tensão Eficaz (VRMS)
Dada uma tensão alternada qualquer, define-se o valor eficaz (VRMS ou VEF) dessa tensão como sendo o valor da tensão CC que produz o mesmo aquecimento que a tensão alternada em questão quando aplciada na mesma resistencia.
Definição matemática
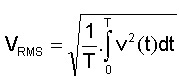
Significado Físico:
O valor eficaz de uma tensão alternada senoidal é igual ao valor da tensão continua que produz mesmo aquecimento
Observe na figura a seguir uma tensão senoidal de valor de pico Vp aplicada a uma resistencia R. A resistencia R vai aquecer (efeito Joule), portanto uma certa potencia P será dissipada na resistencia.
Agora considere a mesma resistencia ligada a uma bateria. Existirá um valor da tensão da bateria para o qual a potencia dissipada será igual a potencia dissipada no circuito em CA. Esse valor (VRMS) é chamado de valor eficaz da tensão alternada de valor de pico Vp.
RMS= Root Mean Square = valor quadrático médio
Obs: Valor de pico=Vp=VM=Valor maximo
Se a tensão aplicada a uma resistencia é senoidal de valor de pico (Vp) o o valor eficaz (VRMS) estarão relacionados por:
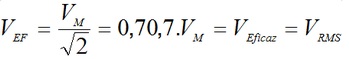
A potencia dissipada em na resistencia em CA pode ser calculada exatamente como em CC somente que devem ser usados valores eficazes, isto é:
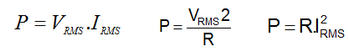
No caso do circuito da Figura 1a como VRMS=110V e R=100 Ohms então a potencia dissipada na resistencia valerá:
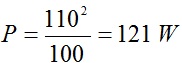
E o valor de pico:
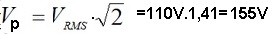
A potencia instantanea, p(t) em CA é obtida pelo produto do valor instantâneo da tensão pela corrente, isto é:
p(t)=v(t).i(t)
Seja uma tensão senoidal de 17 V de pico (12 VRMS) aplicada em uma resistencia de 4 Ohms. Resultará uma corrente senoidal, em fase com a tensão, de 4,25 A de pico e 3 A eficaz. A Figura 2 mostra a forma de onda da tensão instantanea, corrente instantanea e potencia instantanea.
A potencia dissipada será igual ao valor medio da potencia instantanea, linha vermelha no grafico de p(t).
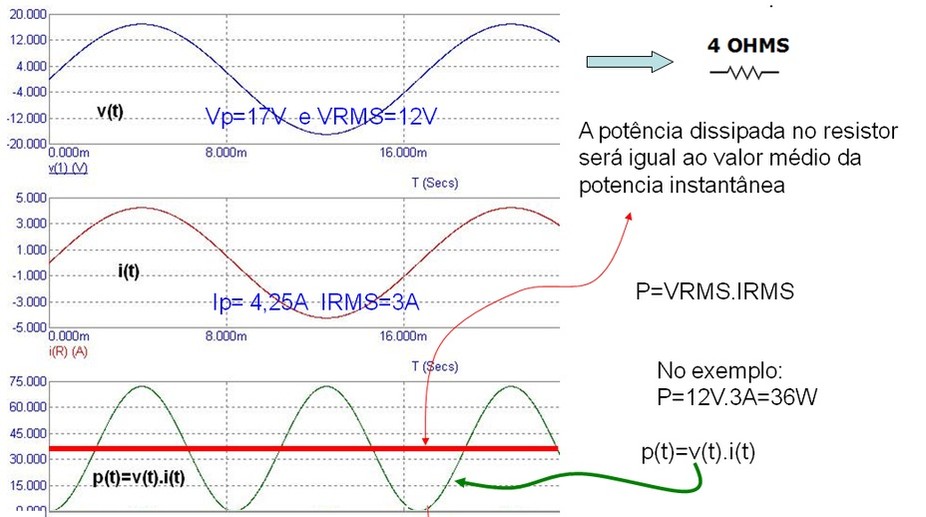
Figura 2 - Potencia em circuito puramente resistivo - formas de onda de v(t), i(t) e p(t)
Importante observar que a potencia é sempre positiva significando que é sempre fornecida pelo gerador. Observar tambem que a potencia é pulsante e de frequencia o dobro da tensão.
Genericamente a potencia que um gerador entrega para um circuito em Watts (W) é dada por:
P=VRMS.IRMS, cosf Expressão super importante
Onde
VRMS=valor eficaz da tensão (V)
IRMS=valor eficaz da corrente (A)
P=potência real, potencia util ou potencia ativa (W)
f é o angulo de defasagem entre a tensão e a corrente no circuito
No caso de um circuito puramente resistivo, f=0 e portanto cosf=1 e nesse caso a expressão fica simplificada:
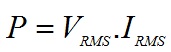
Como já era esperado!
3. Experiência: Circuito resistivo em CA
3.1. Abra o arquivo ExpCA04_Circuito_Resistivo_em_CA (Multisim 14)e identifique o circuito da Figura 3. Inicie a simulação e meça a tensão, a potencia e a corrente no circuito. Anote os valores na tabela 1.
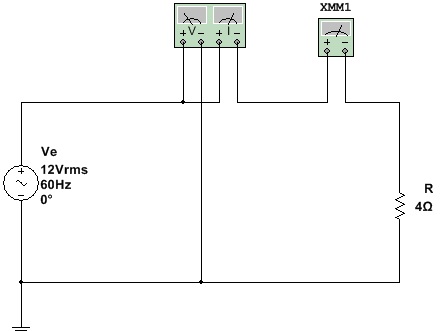
Figura 3 - Circuito resistivo em CA - Medindo potencia e corrente
Clique para acessar o arquivo Multisim Live
Tabela 1 - Circuito resistivo em CA
| Valores teoricos (calculados) | Valores medidos | ||||
| VRMS | IRMS | P(W) | VRMS | IRMS | P(W) |
3.2. Compare com os valores medidos com os calculados.
3.3. Repita os itens anteriores para R=10 Ohms e R= 1k
3.4. Escreva as suas conclusões.
4. Valor médio de uma tensão (VCC)
Define-se valor médio de uma tensão como sendo:
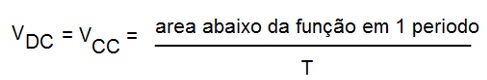
ou matematicamente. Se voce não conhece calculo Integral não temproblema.
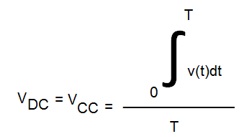
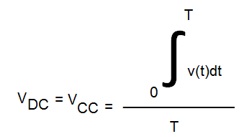
O valor médio (VCC, VDC, VAV) de uma tensão é medido com um voltímetro para CC.
Exemplo1: Qual o valor médio de uma tensão senoidal?
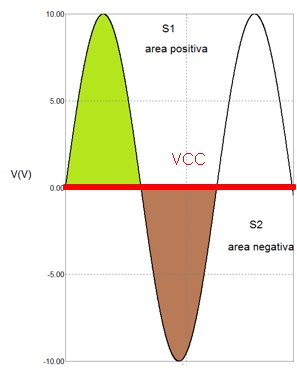
Figura 4 - Valor medio de uma tensão senoidal
As duas áreas são iguais mas uma é positiva e a outra é negativa logo o valor medio é zero:
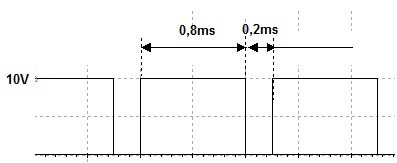
Exemplo 2: dada a onda quadrada determinar:
a) Qual o ciclo de trabalho?
a) Qual o ciclo de trabalho?
b)Qual o valor médio?
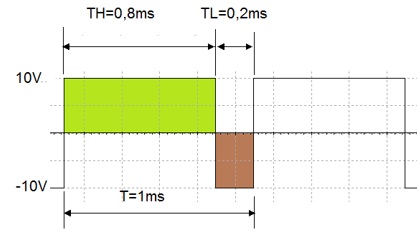
Figura 5 - Valor medio e ciclo de trabalho de uma onda quadrada
Solução:
a) Ciclo de trabalho ou Duty Cicle (D.C) é definido como sendo
Onde TH é o tempo que a tensão permanece em nivel alto e T é o periodo.
Relembrando!
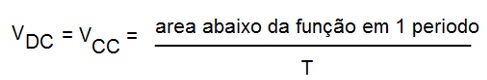
Area positiva (verde)=0,8ms.10V=8V.ms
Area negativa (marrom)=0,2ms.-10V= -2V.ms
como 0 periodo vale T=1ms logo
Area negativa (marrom)=0,2ms.-10V= -2V.ms
como 0 periodo vale T=1ms logo
Area abaixo da função em 1 periodo= 8V.ms - 2V.ms=6V.ms
O valor medio dessa tensão vale:
VCC= 6V.ms/1ms=¨6 V
Esse é o valor que será medido por um voltimetro para CC.
Esse é o valor que será medido por um voltimetro para CC.
Arquivo Multisim - Exemplo 2
5 Exercicios Propostos
5.1 Uma tensão v(t)=10.sen(37.t+600)(V) é aicada a uma resistência de 20 Ohms. Determinar:
a) Expressão de i(t)
b) Desenhar o DF
5.2 Para a onda quadrada determinar:
a) Qual o ciclo de trabalho?
b)Qual o valor médio ?
Considerar:
eixo vertical está calibrado em 2V/divisão e o
eixo horizontal em 500μs/divisão
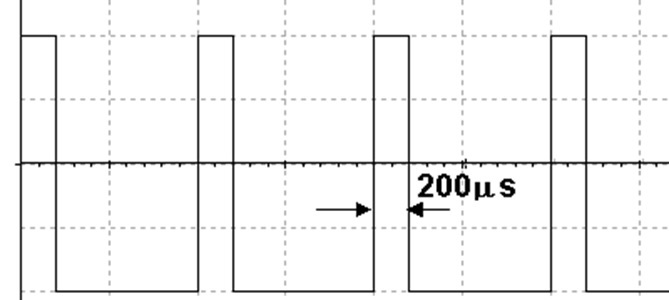
Arquivo Multisim - Exercicio Proposto 5.2
5.3 Determinar o valor medio da tensão e o ciclo de trabalho
Arquivo Multisim - Exercicio Proposto 5.3
5.4 Na questão 5.3 considere que o periodo é o mesmo mas o D.C=50%.
Qual o novo valor medio?
5.5 Na questão 5.3 considere que o periodo é o mesmo mas o D.C=20%.
Qual o novo valor medio?
Para maiores esclarecimentos consultar o Livro Analise de Circuitos em Corrente Alternada Capitulo2