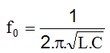aulaCA012 - eletronica24h
Menu principal:
aulaCA012
Educacional > Cursos > Eletricidade em CA
Analise de Circuitos em Corrente Alternada
Aula 12: Circuito RLC Serie - Ressonância
Bibliografia
Analise de Circuitos em Corrente Alternada - Saraiva/Erica
1 Circuitos RLC serie
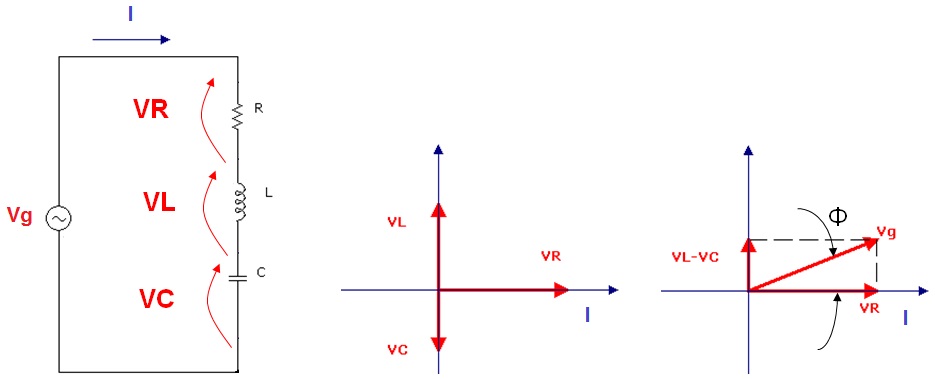
Para analisar o circuito RLC serie, Figura 1a, deve ser lembrando que a tensão total aplicada, Vg, é a soma vetorial das tensões VC, VR e VL. No diagrama fasorial, Figura 1b, a tensão na resistência está em fase com a corrente, a tensão na indutância está adiantada de 90º enquanto a tensão no capacitor está atrasada de 90º. Considerando que a fase da corrente é nula (arbitrariamente), consequentemente todos os outros fasores estarão atrelados a isso. Por exemplo a fase de VR será zero tambem.
( a ) ( b ) ( c )
Figura 1 - ( a ) Circuito RLC serie ( b ) Diagrama Fasorial ( c ) Diagrama Fasorial apos somar VL com Vc
Figura 1 - ( a ) Circuito RLC serie ( b ) Diagrama Fasorial ( c ) Diagrama Fasorial apos somar VL com Vc
No diagrama da Figura 1 considerando, arbitrariamente, que o circuito é indutivo, e portanto VL > VC, e desta forma a corrente estará atrasada em relação à tensão total, Vg. Para obter a tensão total deve-se fazer a soma vetorial das três tensões, como indicado na Figura 1c.
Obs: Na Figura 1b, observe que VL e VC tem mesma direção mas sentidos oposto, logo a resultante da operação VL - VC terá o sentido de VL pois estamos admitindo circuito indutivo .
1.1 Impedancia complexa
A impedancia, Z, do circuito da Figura 1 é obtida somando a resistencia, R, com a reatancia indutiva, XL, e com a reatancia capacitiva, XC, isto é:
Z=R + jXL- jXc=R+ j(XL- Xc)
que é a impedancia complexa na forma cartesiana. O seu modulo é calculado por:
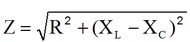
A fase da impedancia, f, é calculada por:
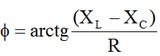
Da Figura 1c tambem é obtido o triangulo das tensões, que relaciona as 4 tensões no circuito:
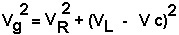
O fator de potencia, cosf, é calculado por:
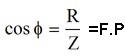
O circuito pode ser resistivo, indutivo ou capacitivo, depende dos valores de XL e Xc.
1.2 Ressonancia
Existe uma freqüência chamada de freqüência de ressonância (fo) para a qual o circuito é puramente resistivo. Nessa freqüência XL= XC sendo calculada por:
Neste caso a impedancia do circuito vale: Z=R o circuito é puramente resistivo, logo cos f=1.
1.3 Comportamento grafico
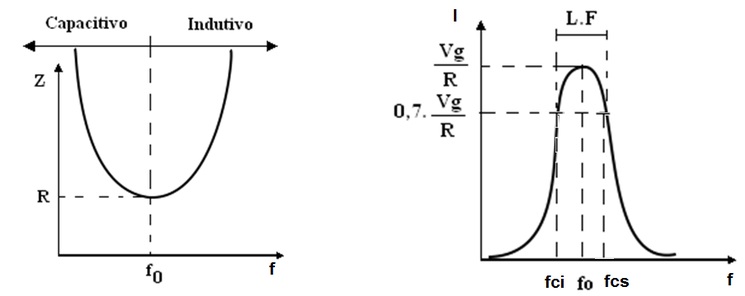
O que acontece com a impedancia, Z, quando a frequencia varia de 0 a infinito? Ao mesmo tempo o que acontece com a corrente? Os gráficos da Figura 2 respondem a essas perguntas.
( a ) ( b )
Figura 2 - Circuito RLC serie ( a ) curva da impedancia em função da frequencia (Zxf) ( b ) curva da corrente em função da frequencia (Ixf)
O grafico da Figura 2a mostra o comportamento do circuito para tres situações:
Na ressonancia, XL=Xc, a impedancia é igual a R e minima, portanto a corrente é máxima e vale Vg/R, Figura 2b.
Se a frequencia for maior que a de ressonancia, XL>Xc, o circuito é resistivo/indutivo, a impedancia aumenta e a corrente diminui.
Caso a frequencia seja menor que a de ressonancia XL<Xc, e o circuito é resistivo/capacitivo, novamente a impedancia aumenta, e a corrente diminui.
Na ressonancia, XL=Xc, a impedancia é igual a R e minima, portanto a corrente é máxima e vale Vg/R, Figura 2b.
Se a frequencia for maior que a de ressonancia, XL>Xc, o circuito é resistivo/indutivo, a impedancia aumenta e a corrente diminui.
Caso a frequencia seja menor que a de ressonancia XL<Xc, e o circuito é resistivo/capacitivo, novamente a impedancia aumenta, e a corrente diminui.
No grafico da Figura 1b define-se a largura de faixa (L.F) ou banda passante, como sendo:
L.F=fcs - fci, onde fcs é a frequencia decorte superior, já definida nos FPA e FPB e fci é a frequencia de corte inferior.
L.F=fcs - fci, onde fcs é a frequencia decorte superior, já definida nos FPA e FPB e fci é a frequencia de corte inferior.
1.4 Fator de Qualidade (Q)
É uma figura de merito da bobina e tambem do circuito. Define-se o fator de qualidade da bobina como sendo:
Define-se para o circuito um fator de qualidade.
Quanto maior for a qualidade da bobina (Q alto), mais seletivo será o circuito. A Figura 3 mostra dois graficos com Q diferentes. O circuito com maior Q é mais seletivo. Como voce pode ver o grafico representa a curva de resposta em frequencia de um filtro passa faixas (FPF).
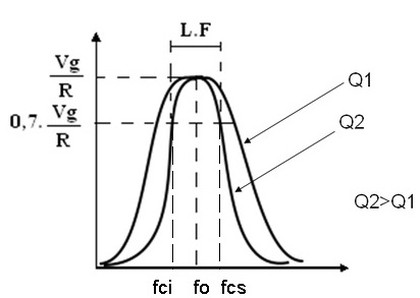
Figura 3 - Curva de resposta em frequencia de dois circuitos RLC com fator de qualidade diferentes
Não será estudado, mas um circuito RLC muito usado é o paralelo que é usado para sintonizar emissoras de radio. O estudo dos circuitos paralelo se encontra na Referencia (Analise de Circuitos em Corrente Alternada - ALBUQUERQUE, R.O. Erica/Saraiva).
1.5 Exercicio resolvido 1
Para o circuito determinar:
a) Freqüência de ressonância
b) Corrente na ressonância (Vg=10 V)
c) Corrente em 5 kHz l
a) Freqüência de ressonância
b) Corrente na ressonância (Vg=10 V)
c) Corrente em 5 kHz l
d) Corrente em 200 kHz
e) Curvas de resposta em frequencia do modulo e da fase
f) Largura de faixa e Fator de Qualidade (Q)
g) Frequencias de corte
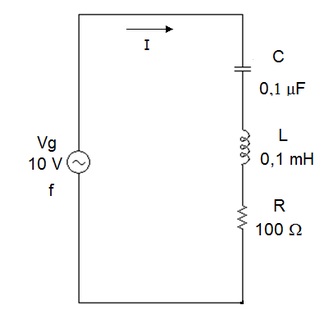
Figura 4 - Circuito para exercicio resolvido
Solução:
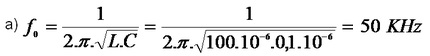
b) Na ressonancia Z=R=100 W logo I = 10 V/ 100 W =0,1 A =100 mA o circuito é resistivo.
c) Na frequencia de 5 kHz a impedancia Z vale:
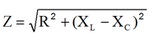
Onde
R= 100 Ohms
 | ||
 |
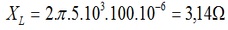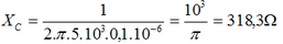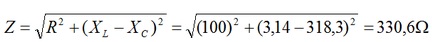
I=10V/330,6 Ohms = 30 mA
d) Na frequencia de 200 kHz Z vale:
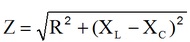
Onde R= 100 Ohms Use calculador para confirmar
 |
 |
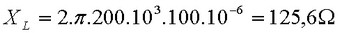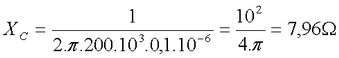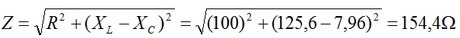
Logo: I=10V/154,4 Ohms= 64,7 mA
2 Experiência: Circuito RLC Série - Medidas das tensões e corrente
2.1 Abra o arquivo ExpCA20 Circuito RLC serie medidas de V e I e identifique o circuito da Figura 5. Observe que o mesmo é o circuito do exercício resolvido anteriormente.
2.2 Ajuste a freqüência do gerador de tensão, Vg, para a freqüência de ressonância ( f0 ). Inicie a simulação em seguida meça a corrente, I, e as tensões VR, VC e VL. Anote esses valores na tabela 1. A partir dos valores medidos das tensões calcule a tensão total (VR+VC+VL) e anote na tabela 1, compare com o valor do gerador (10 V).
Arquivo Multisim Live
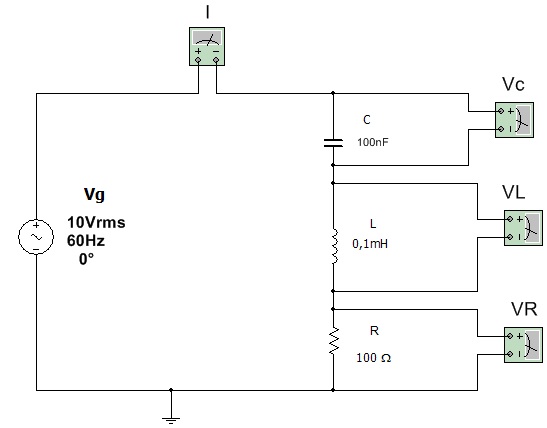
Figura 5 - Circuito RLC serie - medida das correntes
Tabela 1 - Medidas na frequencia de ressonancia
| Medidas na frequencia de ressonancia (f0) | ||||
| I(mA) | VR(V) | VC(V) | VL(V) | VR+VC+VL(V) |
2.3. Repita o procedimento do item 2.2 para f=5 kHz. Anote os valores medidos na tabela 2.
Tabela 2 - Medidas na frequencia de 5 kHz
| Medidas na frequencia de 5 kHz | ||||
| I(mA) | VR(V) | VC(V) | VL(V) | VR+VC+VL(V) |
2.3. Repita o procedimento do item 2.2 para f=200 kHz. Anote os valores medidos na tabela 3.
Tabela 3 - Medidas na frequencia de 200 kHz
| Medidas na frequencia de 200 kHz | ||||
| I(mA) | VR(V) | VC(V) | VL(V) | VR+VC+VL(V) |
2.4 Escreva as suas conclusões.
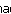t=_____ =_________ A corrente está ____________ ( em fase / atrasada / adiantada ) em relação à tensão.
Figura 7 - Circuito RLC serie para experiencia ( b ) determinando a frequencia de ressonancia
f 0 = ____________ fCI = ____________ f CS = _________ LF = fCS - fCI = _______________
Q = XL0 /R = _____
3 Experiência: Circuito RLC Série - Formas de onda
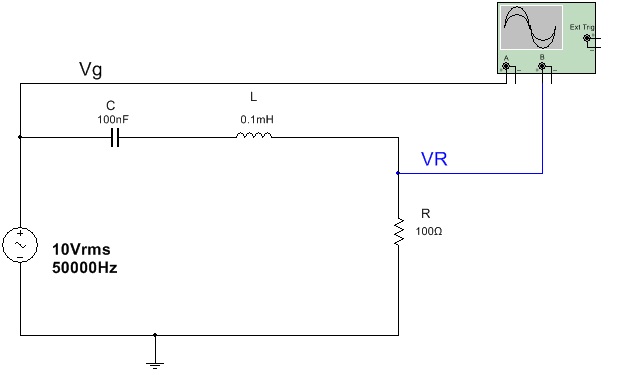
3.1 Abra o arquivo ExpCA21 Circuito RLC serie formas de onda e identifique o circuito da Figura 6 . Ajuste o gerador na freqüência de ressonância. Anote as formas de onda da tensão do gerador, Vg, e da tensão em R, VR, que éstá em fase com a corrente no circuito. Meça a defasagem no tempo (D t) entre as duas e anote. Calcule a defasagem em graus. Anote.
t=_____ f =_________ A corrente está ____________ ( em fase / atrasada / adiantada ) em relação à tensão.
Figura 6 - Circuito RLC serie - defasagem entre corrente e tensão - formas de onda
3.2. Ajuste o gerador em 5 kHz. Anote as formas de onda da corrente e da tensão. Meça a defasagem no tempo entre as duas e em seguida calcule a defasagem em graus .
t=_____ =_________ A corrente está ____________ ( em fase / atrasada / adiantada ) em relação à tensão.
3.3. Ajuste o gerador em 200 kHz. Anote as formas de onda da corrente e da tensão. Meça a defasagem no tempo entre as duas e em seguida calcule a defasagem em graus.
t=_____ =_________ A corrente está ____________ ( em fase / atrasada / adiantada ) em relação à tensão.4 Experiência: Levantamento experimental da curva de resposta em freqüência
4.1 Abra o arquivo ExpCA22 Circuito RLC curva de resposta e identifique o circuito da Figura 7. Inicie a simulação. Abra o Traçador do Diagrama de Bode ou execute uma analise AC caso conheça. Meça o valor da freqüência de ressonância (colocando o cursor de forma que o ganho seja máximo ).
4.2 Da mesma forma determine as freqüências para as quais o ganho será 70,7% menor que na freqüência de ressonância, isto é, 3 dB menor do que na ressonância. Anote essas freqüência como fCI e fCS.
Arquivo Multisim Live
Figura 7 - Circuito RLC serie para experiencia ( b ) determinando a frequencia de ressonancia
Anote os valores obtidos usando o Traçador do Diagrama de Bode :
4.3. Estime a LF por: LF=f0 /Q = ________
Onde
Q é o fator de mérito do circuito calculado por:
Onde
Q é o fator de mérito do circuito calculado por:
Onde
XL0 = reatância do indutor na freqüência de ressonância e
R é a resistência do circuito, no circuito 100 Ohms.
R é a resistência do circuito, no circuito 100 Ohms.
4.3. Varie o valor da freqüência do gerador de acordo com a tabela 4. Para cada valor da freqüência da tabela 4 meça a tensão na saida Vs. Calcule o ganho, Vs/Ve, anotando na tabela 4.Levante o gráfico de 20.log(Vs/Ve)xf em papel monolog, obtendo o valor da freqüência para a qual o ganho é máximo. Anote esse valor como f0. Compare com o valor teórico.
Tabela 4 - Curva de resposta em frequencia - levantamento de dados
| f(kHz) | 10 | 20 | 30 | 45 | 50 | 60 | 80 | 100 | |
| Vs(V) | |||||||||
| Vs/Ve | |||||||||
| 20.logVs/Ve |
4.4 Escreva as suas conclusões.
Para maiores esclarecimentos consultar o Livro Analise de Circuitos em Corrente Alternada Capitulo 4.4