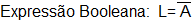aulaDC01 - eletronica24h
Menu principal:
aulaDC01
Educacional > Cursos > Digital Combinacional
ELETRÔNICA DIGITAL - CIRCUITOS COMBINACIONAIS
AULA 01: Funções Booleanas Básicas - Portas Lógicas Básicas
Prof Me. Romulo Oliveira Albuquerque
1. Conceito de Variável Booleana
Variável Booleana é uma variável que pode assumir só duas condições (dois valores). Um exemplo de variável Booleana é uma chave, que só pode estar aberta ou fechada, não existe outra condição. Outro exemplo é uma lâmpada, que só pode estar acesa ou apagada.
Em eletrônica digital costumamos associar a uma variável Booleana os símbolos “ 0 “ e “1 “aos estados que a variavel pode assumir. Desta forma lâmpada acesa poderia ser “1 “ e conseqüentemente apagada “ 0 “, mas poderia ser o contrario depende da convenção adotada.
Uma variável Booleana pode ser dependente de outras variáveis Booleanas. Por exemplo em resposta à condição de uma chave (variável A) a qual pode estar aberta ou fechada podemos ter a condição de uma lâmpada (variável L) acesa ou apagada.
Em eletrônica digital costumamos associar a uma variável Booleana os símbolos “ 0 “ e “1 “aos estados que a variavel pode assumir. Desta forma lâmpada acesa poderia ser “1 “ e conseqüentemente apagada “ 0 “, mas poderia ser o contrario depende da convenção adotada.
Uma variável Booleana pode ser dependente de outras variáveis Booleanas. Por exemplo em resposta à condição de uma chave (variável A) a qual pode estar aberta ou fechada podemos ter a condição de uma lâmpada (variável L) acesa ou apagada.
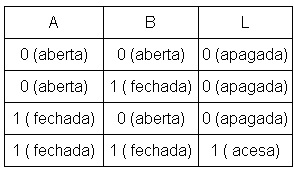
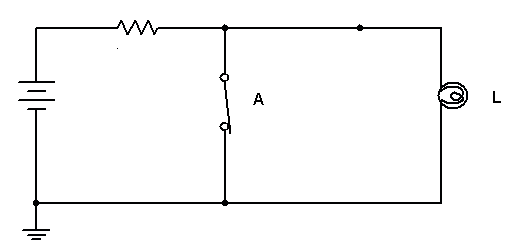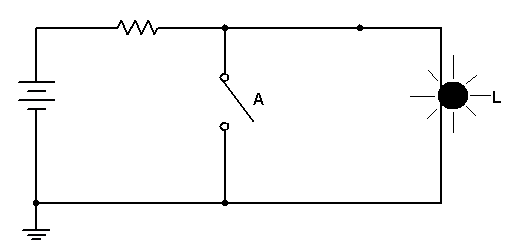
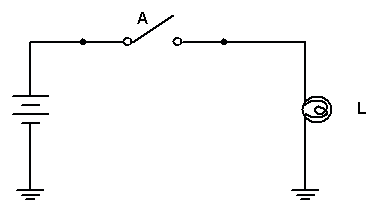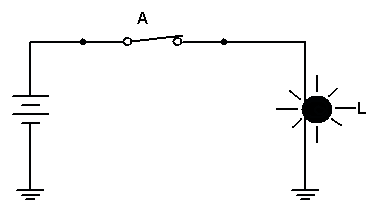
Na Figura 1 podemos convencionar que chave aberta A=0, a chave fechada portanto será A=1 da mesma forma teremos para lâmpada apagada L=0 e acesa L=1.
Para caracterizar o comportamento lógico estabelecemos o que chamamos de tabela verdade do circuito.
Expressão Booleana: L=A
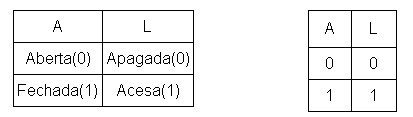
( a ) ( b )
Figura 1 - ( a ) Circuito com chaves ( b ) tabela verdade (TV)
2. Elementos de Álgebra Booleana
Em álgebra Booleana assim como na álgebra comum, as letras são usadas para representar as variáveis. Na Álgebra Booleana usamos letras maiúsculas para representar uma variável Booleana. Uma variável Booleana só pode ter duas condições às quais associaremos os símbolos "0" ou "1".
O símbolo = tem usualmente o significado de "'é equivalente", isto é, se o lado direito da equação é 0, então o lado esquerdo também será 0. Desta forma a declaração:
O símbolo = tem usualmente o significado de "'é equivalente", isto é, se o lado direito da equação é 0, então o lado esquerdo também será 0. Desta forma a declaração:
Y=A significa que Y é 1 se A é 1, Y é 0 se A for 0.
Na Figura 1 é usado uma chave, que representa a variável A se relacionando com a variável L (lâmpada) pela expressão:
L=A (observe isso na tabela verdade)
O símbolo Booleano com uma barra acima da variável significa a negação ou o complemento da variável.
Obs: Para simplificar, ao inves de colocar a barra em cima, será usado um traço A'. Então A linha significa A barra
| A'= |  | |||||||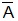
| Desta forma | 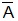| é lido como não A, portanto se A=1 | 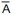 | =0 e se A=0 | 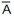 | =1 | ||
3 Funções Booleanas e Portas Lógicas
Uma função Booleana relaciona duas ou mais variáveis Booleanas, de entrada, através de uma expressão chamada de Expressão Booleana, com uma variavel Booleana de saida. Para se implementar na pratica uma função booleana são usadas portas logicas encontradas em C.Is Circuitos Integrados).
3.1 Função E (AND) - Porta E (AND)
Antigamente os circuitos lógicos eram feitos (implementados) com relés, hoje são usadas portas lógicas em C.I (Circuito Integrado) para realizar uma determinada lógica (determinada função). A seguir as principais funções lógicas e as portas lógicas que realizam a lógica da função.
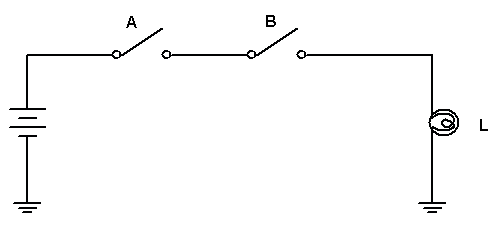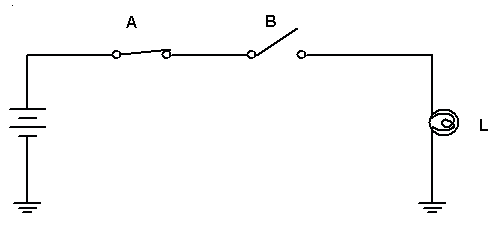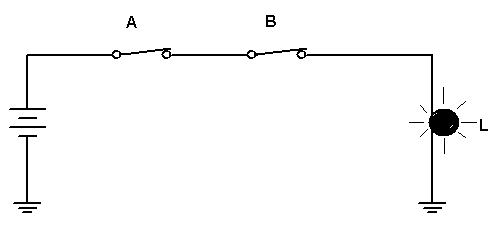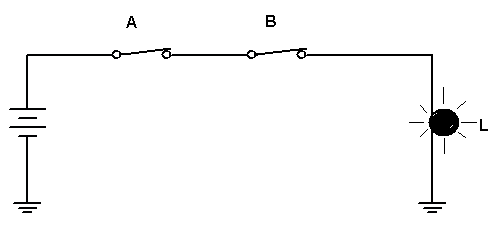
As duas chaves chaves, A e B estão ligadas em série para ligar a lâmpada L.
A lógica existente é:
A lógica existente é:
" A lâmpada acenderá se A E B estiverem fechadas"
Dizemos que esta é uma lógica E (AND em inglês). A porta lógica correspondente é chamada porta E (AND ) e cujo símbolo está representado na Figura 2a.
A Expressão Booleana é: L = A.B (lê-se A e B , mas por analogia com a operação multiplicação dizemos também A vezes B).
A Expressão Booleana é: L = A.B (lê-se A e B , mas por analogia com a operação multiplicação dizemos também A vezes B).
No circuito da Figura 2 a lâmpada acende se a Chave A E a chave B estiverem fechadas ao mesmo tempo.
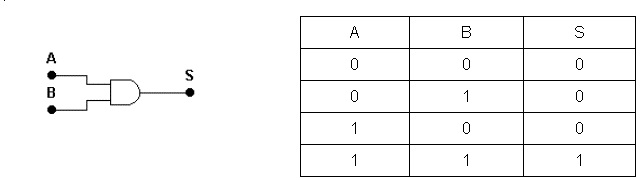
( a ) ( b )
Figura 2 - ( a ) circuito com chaves para lógica E ( b ) Tabela Verdade
A seguir os símbolos da porta E (AND) e a sua Tabela Verdade
( a ) ( b )
Figura 3 - ( a ) Simbolo da porta lógica E (AND) ( b ) Tabela Verdade
3.2. Função OU (OR) - Porta OU (OR )
A função OU (OR ) tem a seguinte lógica: A lampada é acesa se A ou B estiverem fechadas. Expressão Booleana: L = A+B (Lemos A ou B, mas por analogia com a operação soma dizemos A mais B).
A figura 4a mostra a logica OU com chaves, a Figura 4b o símbolo da porta e a Figura 4c a tabela verdade.A função OU (OR ) tem a seguinte lógica: A lampada é acesa se A ou B estiverem fechadas. Expressão Booleana: L = A+B (Lemos A ou B, mas por analogia com a operação soma dizemos A mais B).
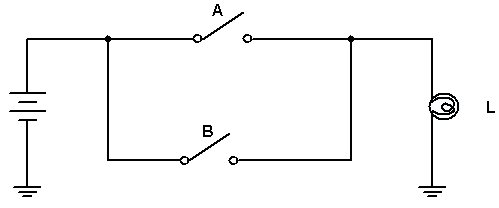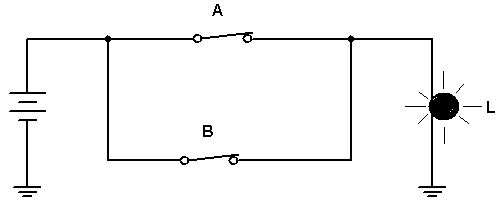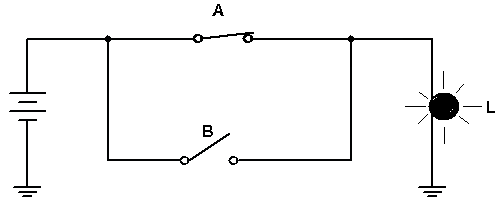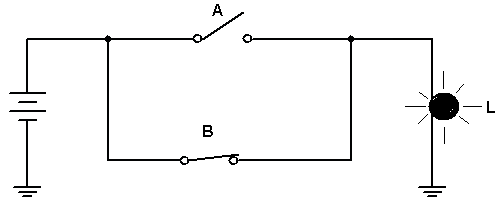
( a )
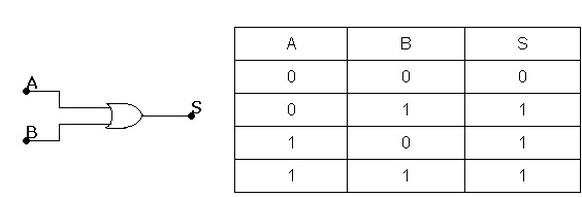
( b ) ( c )
( c )
Figura 4 - Função OU ( a ) circuito com chaves ( b ) Porta OU símbolo ( c ) Tabela verdade
use o link para acessar o arquivo
3.3. Função Inversão Não (NOT) - Porta Inversora
A função Não (NOT) ou função Inversora dá uma saída que é o complemento (inverso) da entrada.
( a ) ( b )
| A | L |
| 0 | 1 |
| 1 | 0 |
( c )
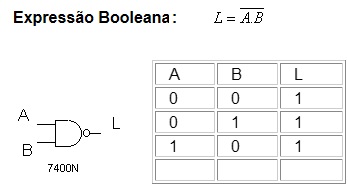
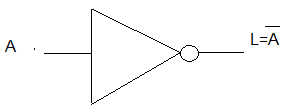
Figura 5 - Função NÃO ( a ) circuito com chaves ( b ) Porta NÃO (NOT) símbolo ( c ) Tabela verdade
use o link para acessar o arquivo
3.4. Mais Propriedades da Álgebra Booleana
A partir do especificado acima (função E, OU e Inversora) resultam algumas relações importantes:
Além disso podem ser usadas algumas propriedades da álgebra ordinária.
3.5. Função NE (NAND) - Porta NE (NAND)
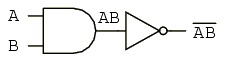
A lógica desta função corresponde à negação da função NE (NAND ). A Figura 6 dá o símbolo da porta lógica e a sua Tabela Verdade .
( a ) ( b )
3.6. Função NOU (NOR) - Porta NOU (NOR)
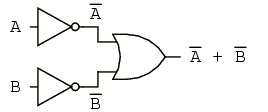
A lógica desta função corresponde à negação da função OU ( NOR ). A Figura 7a mostra o símbolo da porta lógica e a Figura 7b a tabela verdade.
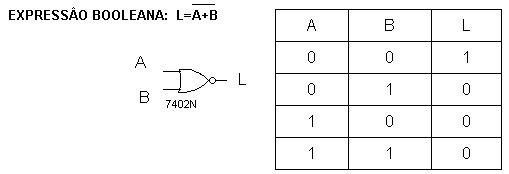
( a ) ( b )
Figura 7 - Porta NOU - ( a ) Símbolo ( b ) Tabela verdade
Use o link para obter o arquivo de simulação
PortaNOU
PortaNOU
4. Teorema de De Morgan
O Teorema de De Morgan é uma ferramenta poderosa usada para simplificar circuitos lógicos e tem como objetivo transformar um produto em uma operação de soma e vice-versa. O matematico chamado De Morgan desenvolveu um par de regras complementares usadas para converter a operação OU em E e vice versa.
Para duas variaveis a lei é:
Ou em termos de portas lógicas:
que é equivalente a:
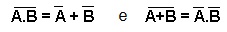
Quando quebramos a barra longa no primeiro termo, a operação abaixo da barra se transforma de multiplicação para soma e vice -versa.
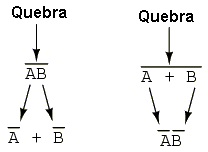
Quando existem varias barras em uma expressão, você deve quebrar uma barra por vez, aplicando a regra cima.
Exemplo1:
A Figura 8 mostra o circuito implementado com portas lógicas e usa 3 CIs diferentes.
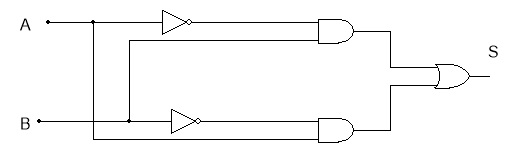
Figura 8 - Exemplificando DeMorgan
A expressão Booleana da saida S é:
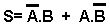
Considere que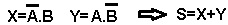 
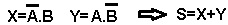ou
ou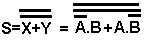
Colocar duas barras não altera a função, isto é:
Trabalhando com a barra maior inferior e aplicando De morgan resulta.
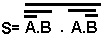
E o circuitp correspondente é o da Figura 9b
Como resultado, o circuito original, Fura 9a, que precisa de 3 CIs pode ser simplificadoa um circuito, Figura 9b, que usa 1 unico CI com 4 portas NAND de duas entradas )7400).
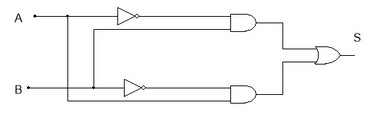
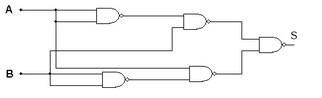
( a ) ( b )
Figura 9 - ( a ) Função obtida com dois tipos de portas usa 3 CIs ( b ) função obtida com um tipo de porta, usa 1 CI
No caso da Figura 9a são usadas duas portas e portanto dois C.Is. No caso da Figura 9b são usadas 4 portas NAND de duas entradas encontradas em um unico CI, o 7400.
4. Experiência: Funções lógicas com chaves
4.1. Abra o arquivo ExpTDC_01_Logica_com_chaves e identifique circuito da figura 10. Inicie a simulação e preencha a TV.
Link para Multisim Live
Tabela verdade Função E com chaves
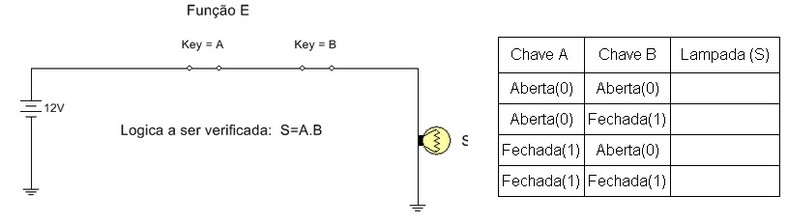
Figura 10 - Circuito com chaves - Função E
4.2. Repita o item 4.1 para o circuito da figura 11.
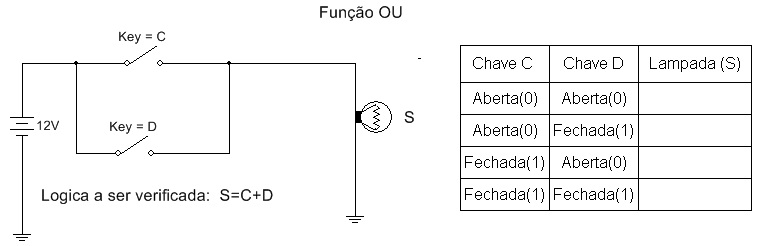
Figura 11 - Circuito com chaves - Função OU e Tabela Verdade
4.3. Repita o item 4.1 para o circuito da figura 12.
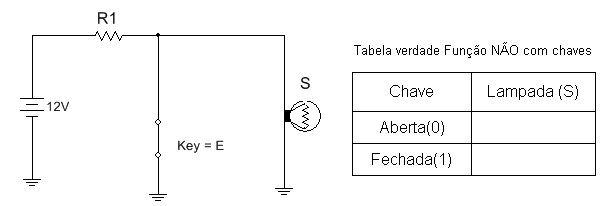
Figura 12 - Circuito com chaves - Função NÃO (INVERSÂO)
4.4. Escreva as suas conclusões.
5.1 Abra o arquivo ExpTDC_02_Portas_Lógicas_Básicas_E e identifique o circuito da figura 13. Verifique o funcionamento para cada combinação da tabela verdade.
Obs: para sinalizar o estado lógico das entradas e da saída existem lâmpadas (Probes) sinalizadoras.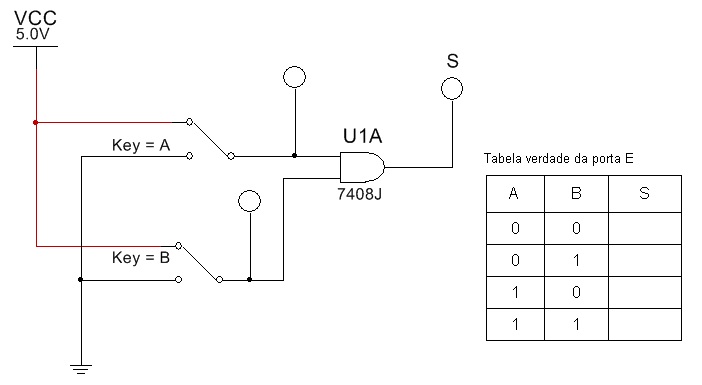Link para Multisim Live
Tabela verdade da porta E
Figura 13 - Porta E Circuito e Tabela Verdade
5.2. Abra o arquivo ExpTDC_03_Portas_Lógicas_Básicas_OU e identifique o circuito da figura 14. Verifique o funcionamento para cada combinação da tabela verdade.
Link para Multisim Live
Tabela verdade da porta OU
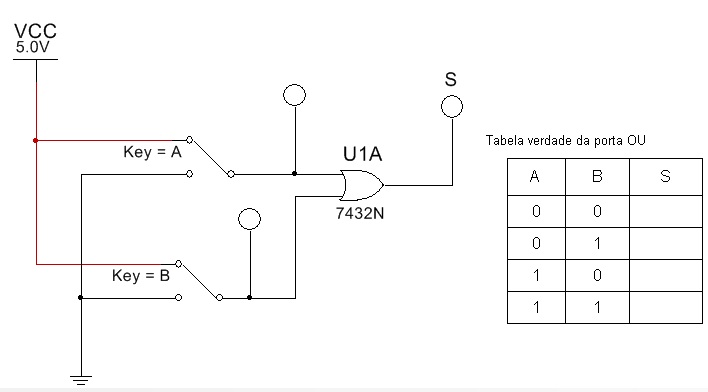
Figura 14 - Circuito para experiencia - Porta OU
5.3. Abra o arquivo ExpTDC_04_Portas_Lógicas_Básicas_NE e identifique o circuito da figura 15. Verifique o funcionamento para cada combinação da tabela verdade.
Link para Multisim Live
Tabela verdade da porta NE
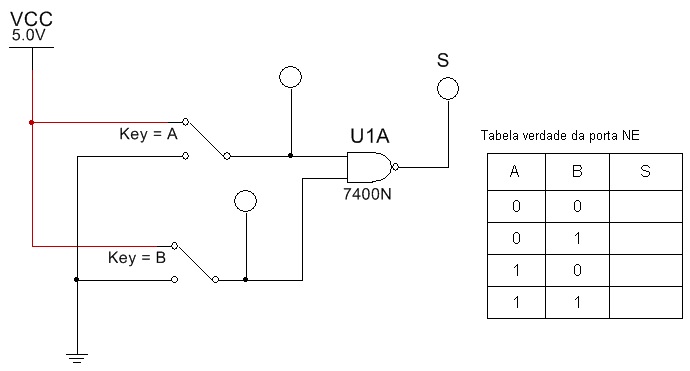
Figura 15 - Circuito para experiencia - Porta NE
5.4. Abra o arquivo ExpTDC_05_Portas_Logicas_Básicas_NOU e identifique o circuito da figura 16. Verifique o funcionamento para cada combinação da tabela verdade.
Link para Multisim Live
Tabela verdade da porta NOU
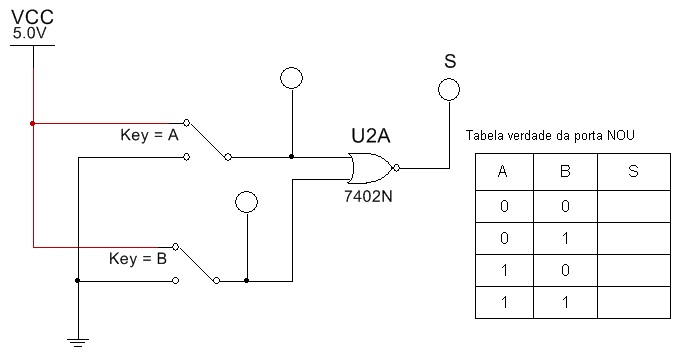
Figura 16 - Circuito para experiencia - Porta NOU
5.5. Abra o arquivo ExpTDC_06_Portas_Logicas_Basicas_NAO e identifique o circuito da figura 17. Verifique o funcionamento para cada combinação da tabela verdade.
Link para Multisim Live
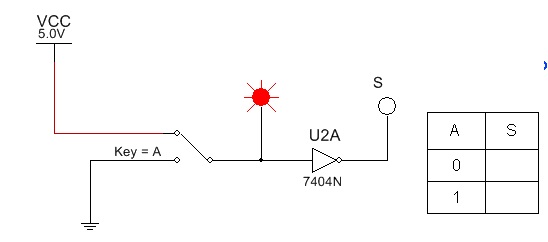
Figura 17 - Circuito para experiencia - Inversor