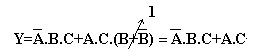aulaDC02 - eletronica24h
Menu principal:
aulaDC02
Educacional > Cursos > Digital Combinacional
ELETRÔNICA DIGITAL - CIRCUITOS COMBINACIONAIS
AULA 02: Funções Booleanas Básicas - Portas Lógicas Básicas
Prof Me. Romulo Oliveira Albuquerque
1. Circuito lógico combinacional - Tabela verdade
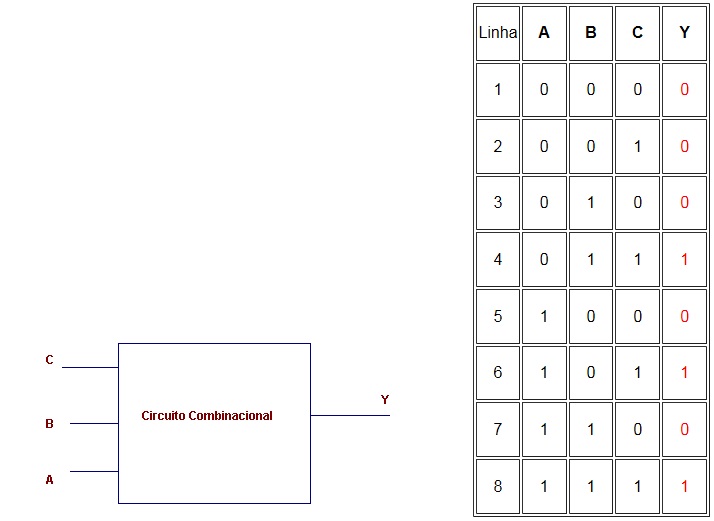
Circuitos logico correspondem à associação de duas ou mais portas lógicas básicas, executando uma determinada função. Para exemplificar, seja um circuito lógico com três variáveis de entrada (ABC) e uma de saída (Y), cuja tabela verdade (TV) é conhecida, Figura 1.
( a ) ( b )
Figura 1 - ( a ) Circuito lógico ( b ) tabela verdade
Observe que a tabela verdade mostra o comportamento do circuito para todas as 8 combinações possíveis das 3 variáveis de entrada. Assim é que na primeira linha A=0 B=0 e C=0 a saída responde com Y=0. Na quarta linha A=0 B=1 e C=1 para as entradas e Y=1 para a saída e assim por diante.
Como implementar (construir) com portas lógicas esse circuito? Qual o circuito? Quantas portas serão necessárias? Quantos Circuito Integrados serão usados?
Como implementar (construir) com portas lógicas esse circuito? Qual o circuito? Quantas portas serão necessárias? Quantos Circuito Integrados serão usados?
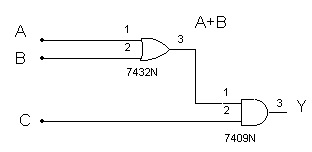
Para construir um circuito são usadas portas lógicas as quais se encontram em CI's. Não existe um único circuito que tenha a mesma TV (portanto que execute a mesma função). Um dos objetivos de se estudar circuito digitais é poder construir um sistema com o menor custo possível. Para o exemplo acima, por exemplo uma possível implementação do mesmo seria o circuito da Figura 2.
Figura 2 - Implementação do circuito logico da tabela verdade da Figura 1b
Atenção!! Observe que serão necessários dois CI's (7432 e 7409), visto que um CI contem somente um tipo de porta lógica.
2. Obtendo a expressão lógica a partir da Tabela Verdade - Soma de Produtos
O circuito da Figura 2 tem a seguinte expressão lógica:
Y=(A+B).C
Essa é a expressão simplificada (mínima).
A expressão máxima (soma de produtos) é obtida através de uma regra bem simples:
Onde a função for "1", pode-se escrever um produto das variáveis de tal forma que esse produto deva ser igual a "1". Por exemplo a linha 4 vale "1", portanto para essa linha escrevemos:
Onde a função for "1", pode-se escrever um produto das variáveis de tal forma que esse produto deva ser igual a "1". Por exemplo a linha 4 vale "1", portanto para essa linha escrevemos:
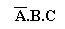
Isto é, para que o produto seja igual a 1 onde a variável for 0 deveremos complementar a variável.
Na linha 6 da mesma forma
Na linha 6 da mesma forma
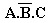
E na ultima linha:
A.B.C
A.B.C
Como a função deve valer 1 para a linha 4 OU linha 6 OU linha 8 então deve ser feita uma operação OU com todos os produtos:
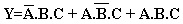
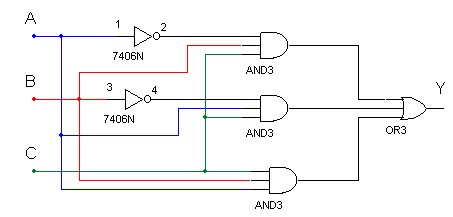
Caso o circuito fosse implementado a partir dessa expressão resultaria o circuito da Figura 3.
Figura 3 - Outra possibilidade para implementar o circuito lógico cuja TV é dada na Figura 1b
Atenção!! Observe que neste caso serão necessários 3 CIs diferentes, 1 para obter os dois inversores, 1 para obter as 3 portas E (AND) de 3 entradas e 1 CI para obter a OU de 3 entradas.
A expressão acima é a máxima e pode ser minimizada usando algumas das propriedades vistas anteriormente. Por exemplo podemos por em evidência C.A nas duas últimas parcelas:
O que resulta outro circuito ( como exercicio, implemente-o), mas é equivalente ao da Figura 3. Para provar isso, obtenha a TV dos dois circuitor.
A expressão mínima pode ser obtida usando uma técnica que usa um mapeamento chamado de Mapa de Karnaugh.
A expressão mínima pode ser obtida usando uma técnica que usa um mapeamento chamado de Mapa de Karnaugh.
3. Obtendo a expressão do circuito
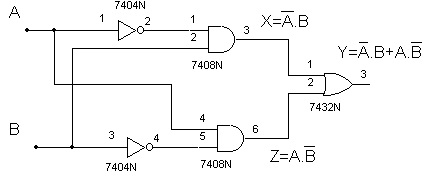
O problema inverso, isto é, o circuito pode ser especificado e deseja-se obter a expressão Booleana (Expressão lógica). Para exemplificar considere o circuito da Figura 4:
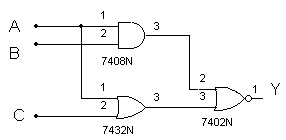
Figura 4 - Circuito para exemplo de como obter a expressão logica
Arquivo Multisim
Para obter a expressão da saída em função das entradas (expressão lógica ou Booleana), a partir das entradas devemos escrever a expressão da saída de cada porta lógica básica encontrada até chegarmos na saída. No exemplo, na saída da porta E de duas entradas A.B = X. A saída da porta OU é A+C =Z. X e Z são as entradas da porta NOU, cuja saída é a saída do circuito.
Portanto
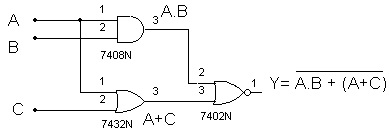
Figura 5 - Circuito da Figura 4 mostrando as expressões parciais e a expressão da saída Y
Para obter a TV do circuito da Figura 5 a saída (Y) para todas as combinações de entrada. Por exemplo se A=B=C=0 qual será o valor da saída ? Veja Figura 6 para compreender isso:
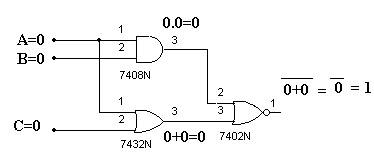
Figura 6 - Circuito da Figura 5 com A=0, B=0 e C=0, resultando Y=1
O que acontece se A=B=C=1 ? Veja figura 7 para compreender isso:
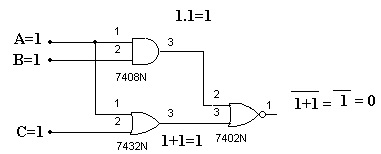
Figura 7 - Circuito da Figura 5 com A=1, B=1 e C=1, resultando Y=0
A primeira e a última linha da TV você já tem. Complete as outras !!
| Ax | Bx | C | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 1 | 1 | 0 |
Exemplo3: Dada a expressão Booleana obtenha o circuito e a TV.
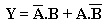

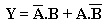
Primeiramente obter o circuito.
A variavel A deve ser invertida e entra em uma porta E com B para obter a primeira parcela. Da mesma forma a variavel B deve ser invertida e entra em uma porta E com A. O resultado vai para uma porta OU conformeCircuito da Figura 8
São necessarias duas portas E, duas inversoras e uma OU, portanto 3 CI's diferentes, Figura 8.

Figura 8 - Implementação do circuito do Exemplo 3 usando varios tipos de portas
Arquivo Multisim Live

O processo para obter a TV já foi visto colocaremos apenas as respostas.
| Bx | A | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
4. Exercícios Propostos
1) Dada a função
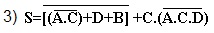
Pede-se: a) Obter a sua TV b) Implementa-la usando portas lógicas.
3) Dada a expressão Booleana S=(A+B).C.(B+D) obter a o circuito.
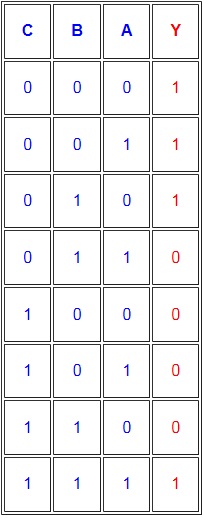
4) Dada a TV de um circuito obter a expressão não minimizada (soma de produtos). Em seguida implemente a função com quaisquer porta lógica.
5. Experiencia: Circuitos combinacionais com qualquer porta
5.1. Abra o arquivo ExpTDC_07_Circuitos_combinacionais1 (Multisim 14) e identifique o circuito da figura 08. Inicie a simulação e em seguida preencha a T.V. Use as chaves para impor "0" e "1", lembrando que lampada apagada="0" lampada acesa="1"
Arquivo Multisim On Line
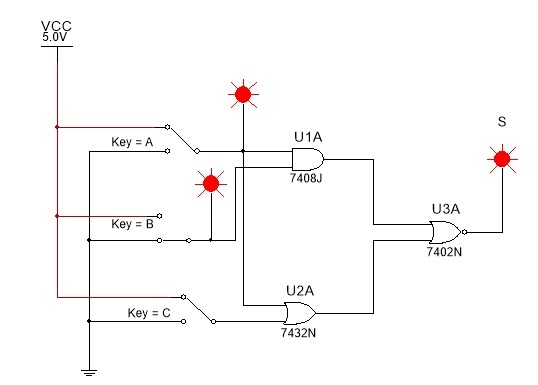
Figura 8 - Circuito para experiencia - Circuito combinacional com portas quaisquer
5.2. Abra o arquivo ExpTDC_08_Circuitos_combinacionais2 (Multisim 14) e identifique o circuito da figura 9. Neste circuito existe um Conversor Logico ligado ao circuito.
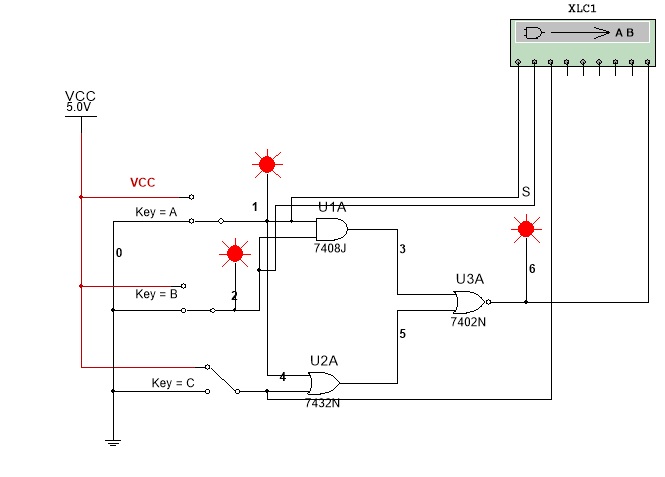
Figura 9 - Circuito digital com Conversor Logico ( Essa ferramenta só existe no Multisim 14)
5.3. Obtenha a tabela verdade clicando no Botão 1 (ver a aula O Conversor Lógico (Logic Converter)) para isso clique no link Conversor Logico. Compare a tabela verdade obtida em 5.1 com a tabela verdade obtida no Conversor Logico.