aulaEN014 - eletronica24h
Menu principal:
aulaEN014
Educacional > Cursos > Eletronica Basica 1
Aula13 Indice de Aulas Aula15
Eletrônica Básica 1
Aula 14: Amplificador Emissor Comum de Pequenos Sinais sem Realimentação
Referencias
MALVINO, Albert. Eletronica V1
ALBUQUERQUE, R.O. ; PINTO, L. F. Eletronica Analogica. V2. São Paulo: Fundação Pe. Anchieta
SEDRA, A. Microeletronica
SEDRA, A. Microeletronica
1. Amplificador de pequenos sinais
Um amplificador de pequenos sinais como o nome diz amplifica pequenos sinais. O que significa pequeno sinal? Um sinal que varia ao redor do ponto Q em um trecho aproximadamente linear das curvas caracteristicas de forma que não apresenta distorção. A Figura 1 mostra um ampliifcador emissor comum tipico para pequenos sinais. Observem os 3 capacitores no circuito, C1 e C2 são chamados de capacitores de acoplamento e tem como finalidade permitir que somente o sinal passe de um ponto para outro bloqueando a componente continua (polarização). O capacitor CE é chamado de capacitor de desacoplamento ou bypass e tem como finalidade desacoplar o emissor em CA (aterrar o emissor em CA). Então antes de estudar o amplificador de pequenos sinais voce aprenderá sobre esses capacitores.
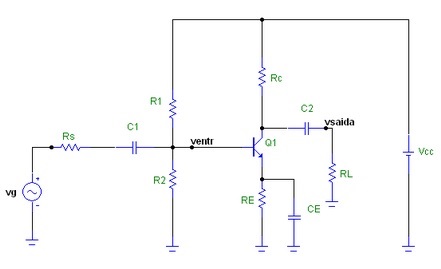
Figura 1 - Amplificador Emissor Comum (AEC) de pequenos sinais
1.1. Capacitores de acoplamento
Um capacitor de acoplamento, acopla um ponto não aterrado a outro ponto não aterrado (acoplar significa deixar passar somente o sinal, bloqueando a componente contínua). Por exemplo no circuito da Figura 2 se o capacitor estiver bem dimensionado (XC << R1 +R2), em RL teremos só a parte alternada da tensão de entrada (Ve) e com amplitude dada pelo divisor de tensão composto por R1 e R2 , isto é, o capacitor terá reatância desprezível face a R1 + R2 na menor freqüência de operação do circuito.
Equações: Para um bom acoplamento XC << RT onde RT= Rs+RL ou
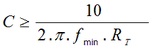
onde fmin é a menor freqüência de operação do circuito, por exemplo se for um amplificador de áudio fmin =20Hz.
Obs: >> significa muito maior, e muito maior é pelo menos dez vezes maior. A Figura 2a mostra um capacitor C acoplando dois pontos 1 e 2. A Figura 2b mostra as formas de onda nos pontos 1 e 2. Observar que no ponto 1 a tensão tem uma componente continua, 4 V. No ponto 2 não existe componente continua e o valor da amplitude depende dos valores de Rs e RL.
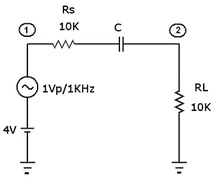
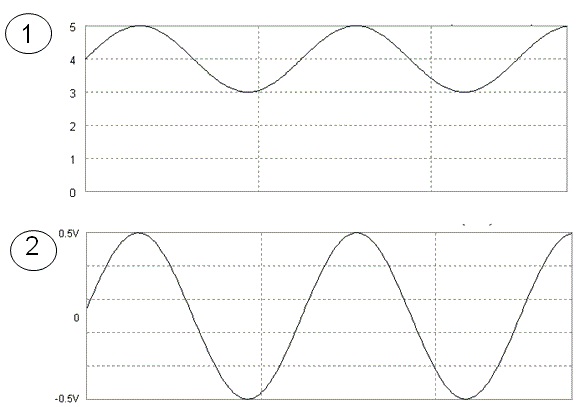
( a ) ( b )
Figura 2 - ( a ) Capacitor de acoplamento acoplando dois pontos não aterrados 1 e 2 ( b ) formas de onda no ponto 1 e no ponto 2
Dimensionamento de C
Para um bom acoplamento a reatancia do capacitor deve ser muito menor que a resistencia total em serie: Xc<<<RT=20 k, isto é, Xc<2 k logo:
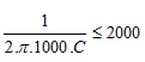
ou
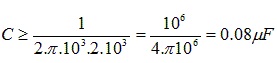
Adotar o valor comercial mais proximo superior C=1 mF
2. Experiencia: Capacitor de acoplamento
2.1. Abra o arquivo ExpEN1_25 Capacitor de acoplamento (Multisim 14) e identifique o circuitos da Figura 2a. Calcule qual o valor estimado da tensão em RL (VS) de pico a pico, e qual a sua forma de onda para C=10 mF. Use a tabela 1 para indicar os valores medidos e calculados
Arquivo Multisim Live
Tabela 1 - Capacitor de acoplamento - C=10 mF
| Valor de VRL | ||
| Calculado (pico a pico) | Medido com osciloscopio (pico a pico) | Voltimetro (RMS) |
2.2. Repita o item 1 considerando agora C = 0,1 mF.Use a tabela 2 para indicar os valores medidos e calculados.
Tabela 2 - Capacitor de acoplamento - C=0,1 mF
| Valor de VRL | ||
| Calculado (pico a pico) | Medido com osciloscopio (pico a pico) | Voltimetro (RMS) |
2.3. Escreva as suas conclusões.
3. Amplificador emissor comum de pequenos sinais
Quando um transistor é polarizado, uma tensão de polarização CC é aplicada à base (VBE) e ao coletor (VCE). Quando um sinal é aplicado à entrada do amplificador a tensão oscilará acima e abaixo de VBE, portanto existirá uma variação de tensão (DVBE) ao redor do ponto quiescente o que provocará uma variação (DIE) de corrente ao redor do valor quiescente.
Atenção!!! Um amplificador é chamado de pequeno sinais se a amplitude do sinal for suficientemente pequena de forma que a operação do mesmo se dá na região linear da curva IExVBE. A Figura 3 mostra um sinal, DVBE, aplicado na base e a resposta, DIE.
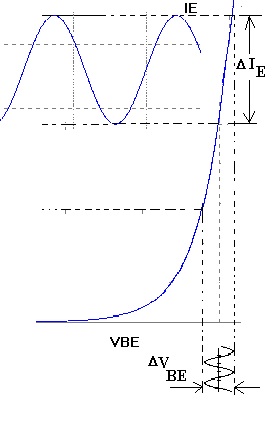
Figura 3 - Curva IExVBE de um transistor
Na Figura 3 define-se a resistência incremental ou resistência dinâmica da junção base emissor como sendo:
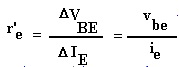
re’ pode ser calculada aproximadamente por:
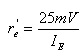
onde IE é a corrente quiescente de emissor e 25 mV é uma constante a temperatura de 25ºC.
A analise dos amplificadores de pequenos sinais que serão feitas a partir de agora usam o modelo simplificado chamado T para determinar os principais parâmetros CA tais como ganho de tensão, impedância de entrada e impedância de saída. Comparado a outros modelos requer pouco calculo e por isso mesmo é indicado. Os resultados não são muito diferentes.
Obs: A resistencia estatica é simplesmente a tensão CC dividida pela corrente CC, isto é, R=V/I
3.1. Modelo simplificado do transistor em baixas freqüências
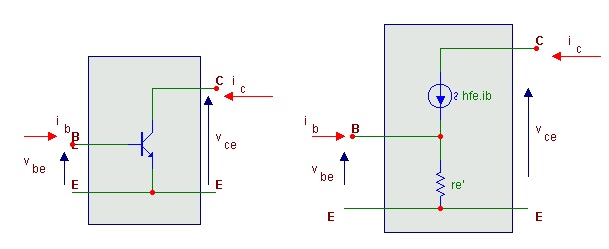
Este modelo (circuito equivalente) é para freqüências baixas, pois não considera as capacitâncias parasitárias, isto é, as capacitancias parasitarias são consideradas em aberto, pois em geral aparecem em paralelo com o transistor. Observe a notação usada par representar um sinal:
ic=ΔIC=variação da corrente de coletor ao redor do ponto Q
ib=ΔIB=variação da corrente de base ao redor do ponto Q
vbe=ΔVBE=variação da tensão base emissor ao redor do ponto Q
vce=ΔVCE=variação da tensão de coletor ao redor do ponto Q
( a ) ( b )
Figura 4 - Circuito equivalente do transistor para baixas frequencias ( a ) sinais de corrente e tensão em um transistor ( b ) Modelo simplificado para pequenos sinais
A analise de um amplificador é dividida em duas partes: O circuito em CC e o circuito em CA. A resposta global no circuito, Figura 4, é a superposição das respostas no circuito CC e circuito CA. A Figura 5 a seguir mostra um estagio amplificador emissor comum completo com os capacitores de acoplamento e desacoplamento e a indicação das tensões em alguns pontos. Observe que a tensão total é composta de uma parte CC e de uma parte CA.
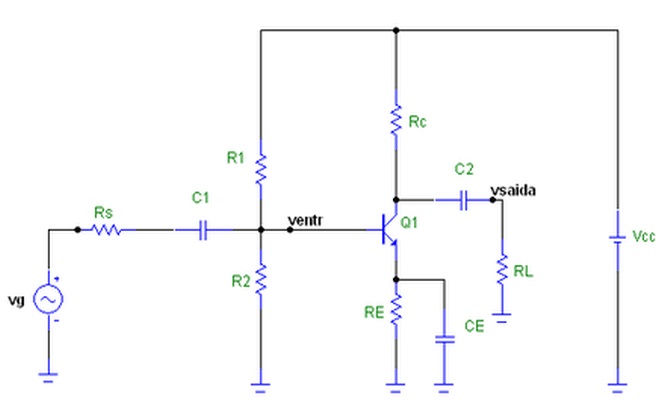
Figura 5 - Amplifciador Emissor Comum completo com a indicação das formas de ondas nos principais pontos
3.2. Circuito equivalente CC de um amplificador emissor comum
Para obter o circuito equivalente para CC, os capacitores deverão ser considerados como circuito aberto. As correntes e tensões presentes no circuitos são contínuas (ponto quiescente). Resulta o circuito da figura 6. A analise deste circuito já foi feita quando o ponto quiescente (polarização) foi calculado.
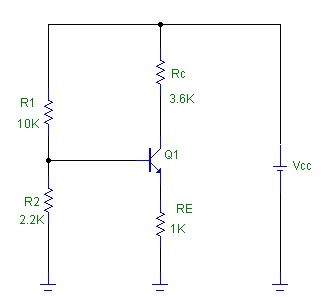
Figura 6 - Circuito equivalente CC do amplificador da figura 5
3.3. Circuito equivalente CA de um amplificador emissor comum para pequenos sinais
Para obter o circuito equivalente para CA, os capacitores e as fontes CC são considerados "curto-circuito" para variações, isto é, a variação de tensão entre seus terminais é zero, ou de outra forma, se for usado um voltimetro CA para medir a tensão nos terminais desses componentes será indicado zero.
As correntes e tensões presentes no circuitos são variações, isto é: DVBE, DVCE DIB, DIE e DIC. Neste circuito deveremos determinar as impedâncias de entrada e saída e os ganho de tensão e corrente.
Tem alguma variação nos terminais da bateria Vcc? Não, a tensão é constante, então dizemos que os seus terminais estão em "curto-circuito" para variações. Então o circuito equivalente para variações é indicado na Figura 7.
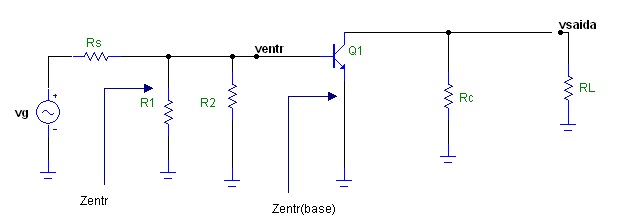
Figura 7 - Circuito equivalente CA (circuito para variações)
3.4. Amplificador EC - Resistência de fonte zero e carga infinita
A analise CA é feita inicialmente considerando o caso em que a resistência da fonte (Rs) de sinal é nula e a carga (RL) ligada na saída é infinita. A Figura 8 mostra o circuito nessas condições.
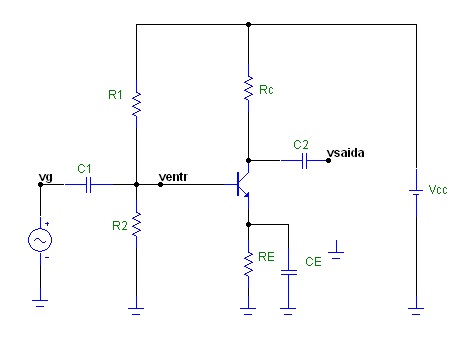
Figura 8 - Amplificador EC com Rs=0 e carga (RL) infinita
Observe que o equivalente CC do circuito da Figura 8 é igual ao da Figura 6 e o circuito equivalente CA está indicado na Figura 9.
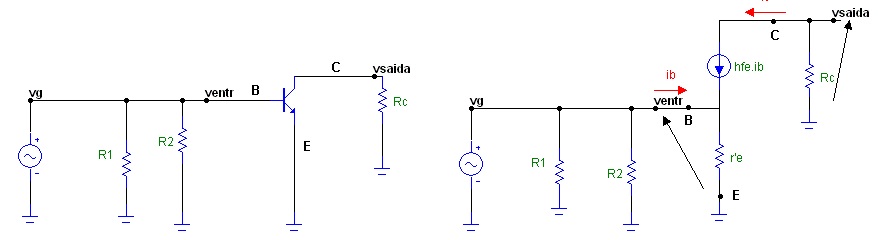
( a ) ( b )
Figura 9 - Circuito equivalente CA do circuito da Figura 8 ( a ) com transistor ( b ) com circuito equivalente do transistor
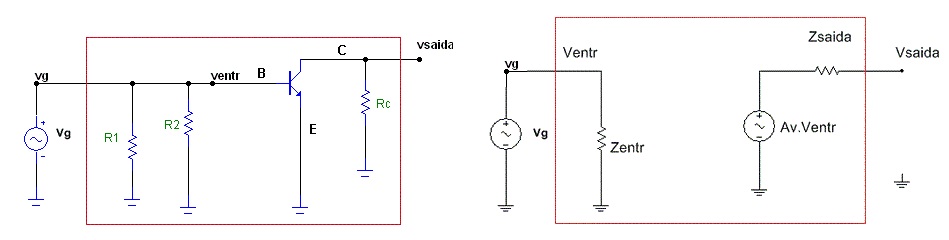
No circuito equivalente CA da Figura 9 o emissor está aterrado pois o capacitor CE é um curto circuito (se estiver dimensionado adequadamente). Os resistores R1 e R2 estão em paralelo pois a bateria é um curto circuito para variações (DV=0). Observar tambem na Figura 9 que o sinal de entrada do gerador de sinais (Vg) é igual ao sinal aplicado na base (Ventr). Para esse circuito a impedância de entrada (Zentr) que o gerador Vg "enxerga" é:
Zentr=R1//R2//Zentr(base) onde
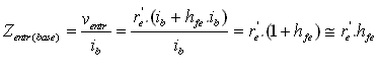
onde hfe é ganho de corrente CA (é o beta CA) que é diferente do beta CC. É um dos parametros do transistor no modelo H (hibrido).
O ganho de tensão entre a saída (Vsaida) e a entrada (Vg=Ventr) é dado por:
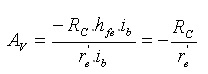
onde re’ é a resistência incremental da junção base emissor definida anteriormente.
O sinal de menos na expressão do ganho indica defasagem de 180º entre a entrada e a saída.
Para a analise CA circuito da Figura 8 pode ser usado o modelo da Figura 10 a seguir para representar a entrada e a saída.
Zentr=R1//R2//Zentr(base) , Zentr(base)=b.re’ Z saida = Rc
E o ganho de tensão:
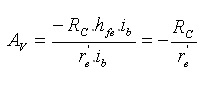
( a ) ( b )
Figura 10 - Circuito equivalente CA do circuito da Figura 9 ( b ) Circuito equivalente CA do circuito da Figura 9 simplificado
O circuito da saida é obtido aplicando Thevenin ao circuito da Figura 9b, na saída.
4. Experiência: Amplificador EC sem resistencia de fonte (Rs=0) e sem carga (RL infinita)
4.1. Abra o arquivo ExpEN1_26_AEC_sem_Rs_e_sem_RL_sem_realimentacao (Multisim 14) e identifique o circuito da Figura 11.
4.2. Inicie a simulação, e calcule o valor de re ’ a partir da medida da corrente quiescente de emissor. Calcule o valor desse parametro usando por:
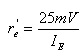
4.3. Calcule o ganho total (AVT=Vsaida/Vg) usando a expressão acima e o fato de que Vg=Ventr. Anote na tabela 3 como AVT(calc).
Adotar b=200 para efeitos de cálculos.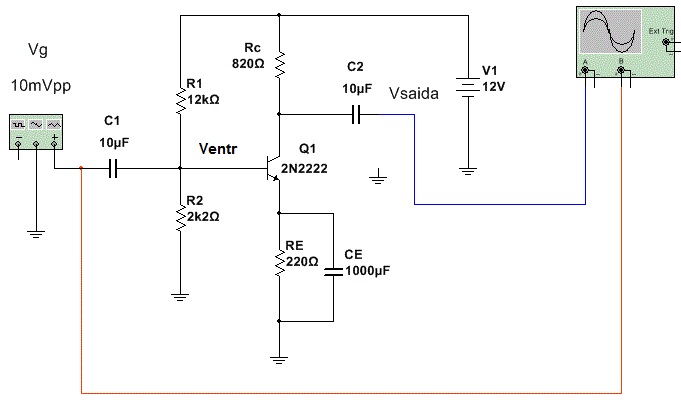
Figura 11 - AEC para experiencia - Resistencia de fonte zero e resistencia de carga infinita
Tabela 3 - Medida do ganho do AEC resistencia de fonte nula carga infinita
| IE(mA) | re’ | Zentr(base) | Zentr | AVT(calc) | Vsaidapp | AVT(Medido) |
4.4. Escreva as suas conclusões.
5. Amplificador EC com resistência de fonte (Rs) e carga (RL)
Observe o amplificador EC da Figura 12. Neste amplificador existe uma resistência da fonte de sinal (que pode representar também a resistência de saída do estágio anterior), Rs, e uma carga (que pode representar a resistência de entrada do estágio seguinte), RL. Observe que o circuito em destaque é o mesmo analisado anteriormente, desta forma podemos usar o mesmo modelo da Figura 9, adicionando a carga (RL) e a resistência da fonte (RS).
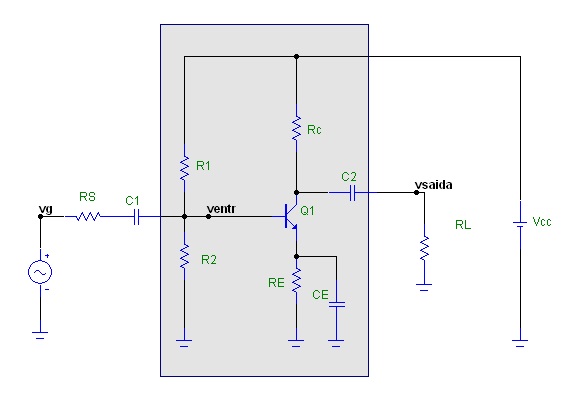
Figura 12 - Amplificador EC com resistência de fonte (Rs) e carga (RL)
Para a analise CA circuito da Figura 12 pode ser usado o modelo da Figura 10b para representar o transistor as resistencias R1, R2 e Rc.
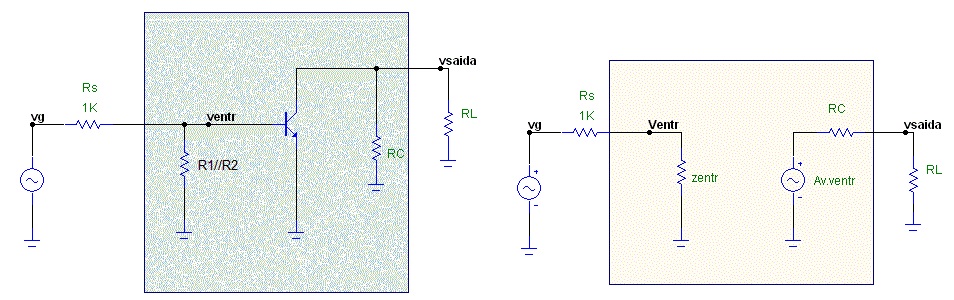
( a ) ( b )
Figura 13 - Circuito equivalente CA para o circuito da Figura 12 ( a ) com transistor ( b ) com circuito equivalente do transistor
A impedância de entrada é calculada da mesma forma que antes, mas a tensão na entrada (Ventr) agora é uma parcela da tensão do gerador Vg (é um divisor de tensão).
Zentr=R1//R2//Zentr(base) e Zentr(base) = b.re’
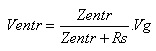
Na saída devido a carga, RL, também tem uma divisão de tensão, e portanto a saída será dada por:
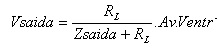
sendo
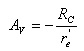
Como
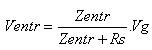
6. Experiência: Amplificador EC com resistencia de fonte (Rs) e com carga (RL)
6.1. Abra o arquivo ExpEN1_27_AEC_com_Rs_e_com_RL_sem_realimentacao (Multisim 14) e identifique o circuito da Figura 14. Use o modelo acima para calcular a tensão de saída (Vsaida) e em conseqüência o ganho. Calcule o ganho total (AVT=Vsaida/Vg) usando a expressão acima e anote na tabela 4 como AVT(calc).
Lembre-se que o ganho Av que aparece na expressão acima é o ganho entre a base e a saída considerando RL infinito sendo dado por:Arquivo Multisim Live
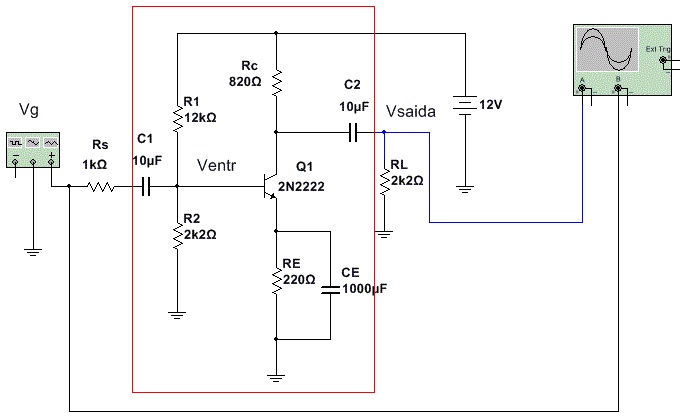
Figura 14 - AEC com resistencia de fonte (Rs) e resistencia de carga (RL)
6.2. Inicie a simulação do circuito e meça a tensão de saída de pico a pico (Vsaídapp) anote na tabela 4, em seguida calcule o ganho experimental, Av(expp) por Vsaídapp/Vgpp.
6.3. Estime a impedância de entrada a partir da medida do sinal na base (ventr), lembrando que, a tensão na base pode ser escrita por: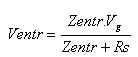
como são dado Vg e RS e é possivel medir ventr então Zentr pode ser calculada.
Obs: Não esquecer que Ventr é somente o sinal variando ao redor da tensão quiescente de base.
Tabela 4 - Medida do ganho do AEC com resistencia de fonte e com resistencia de carga
Ventr | AVT(calc) | Vsaidapp(medido) | Av(exp)=Vsaidapp/40mV | Zentr(estimado) | AVT(Medido) |
6.4. Escreva as suas conclusões.
