aulaEN015 - eletronica24h
Menu principal:
aulaEN015
Educacional > Cursos > Eletronica Basica 1
Aula14 Indice de Aulas Aula16
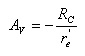
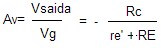
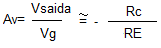
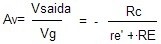
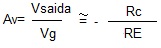
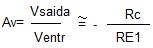
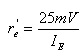
Eletrônica Básica 1
Aula 15: Amplificador Emissor Comum com Realimentação
Referencias
MALVINO, Albert. Eletronica V1
ALBUQUERQUE, R.O. ; PINTO, L. F. Eletronica Analogica. V2. São Paulo: Fundação Pe. Anchieta
SEDRA, A. Microeletronica
SEDRA, A. Microeletronica
1. Amplificador Emissor Comum com Realimentação
Como estudado na aula 14, o amplificador EC sem realimentação tem o ganho dado por:
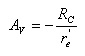
A expressão mostra que o ganho sem realimentação estudado é altamente dependente do parâmetro re’, o qual pode variar de valor por causa do transistor e por causa da temperatura, desta forma o ganho pode se tornar altamente instável. Para tornar o circuito estável e diminuir a distorção é aplicado realimentação negativa em CA.
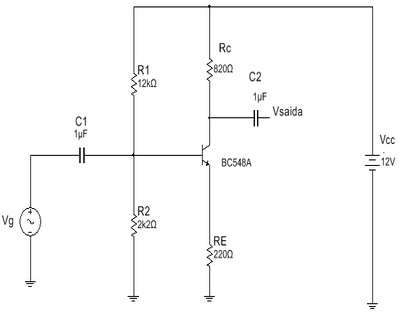
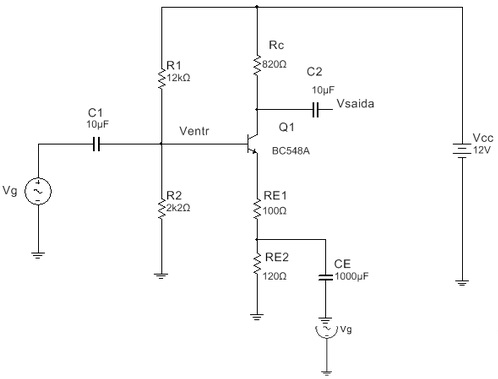
O circuito da Figura 1 é um amplificador EC com realimentação negativa em CA através do resistor RE o qual não tem capacitor de desacoplamento em paralelo, o que causa a realimentação em CA. Essa realimentação (negativa) torna o ganho do circuito menos dependente do parâmetro re’ e diminui a distorção, mas diminui tambem o ganho como será mostrado.Observar que do ponto de vista CC a resistência de emissor é RE.
Figura 1 - Amplificador EC com realimentação negativa
1.1. AEC sem resistencia de fonte e carga infinita - Circuito equivalente em CA
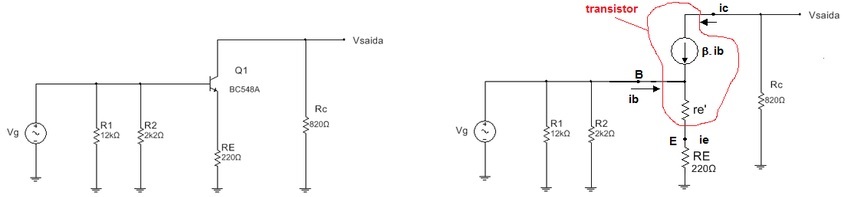
O circuito equivalente para pequenos sinais está indicado na Figura 2. Observar que o capacitor de CE curto circuita a resistência RE2, e portanto ela não aparece no circuito equivalente CA.
( a ) ( b )
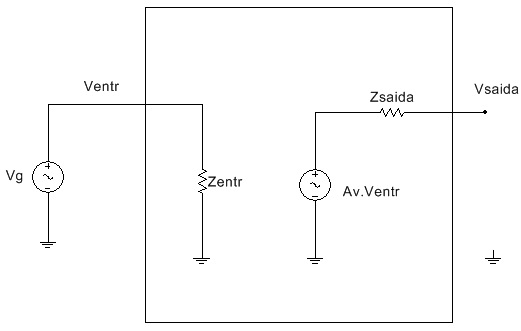
Figura 2 - ( a ) Circuito equivalente CA do amplificador com realimentação da Figura 1 ( b ) equivalente com modelo do transistor
Figura 2 - ( a ) Circuito equivalente CA do amplificador com realimentação da Figura 1 ( b ) equivalente com modelo do transistor
Com relação ao circuito da Figura 2, o resistor RE aparece no circuito equivalente CA (não existe capacitor de desacoplamento em paralelo com o mesmo) e é através dele que aparecerá uma realimentação CA que diminui o ganho, que é dado agora por:
Do ponto de vista CC o circuito é igual ao visto na aula anterior, portanto as correntes quiescentes são iguais. Se RE >>> re’ o ganho será estabilizado e dado por:
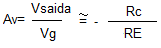
isto é, “o ganho não depende do transistor “, só da relação entre as duas resistências, nessas condições dizemos que a realimentação estabilizou o ganho. Na prática, o ganho varia quando trocamos o transistor, mas é uma variação muito pequena. Isto é, “o ganho não depende do transistor “, só da relação entre as duas resistências, nessas condições dizemos que a realimentação estabilizou o ganho. Na prática, o ganho varia quando o transistor é trocado, mas é uma variação muito pequena.
A analise CA do circuito da Figura 1 e Figura 2 pode ser feita considerando o circuito equivalente CA da Figura 3.
Figura 3 - Circuito equivalente AC do circuito da Figura 1 para freqüências baixas
Para o circuito da Figura 3:
Zentr=R1//R2//Zentr(base)
Onde Zentr(base) = b(re’ + RE )
e
Z saida = Rc
com o ganho dado por:
Observe que Ventr=Vg pois não existe resistencia da fonte de sinal, Vg.
1.2. Amplificador EC com realimentação e com resistência de fonte (Rs) e carga (RL)
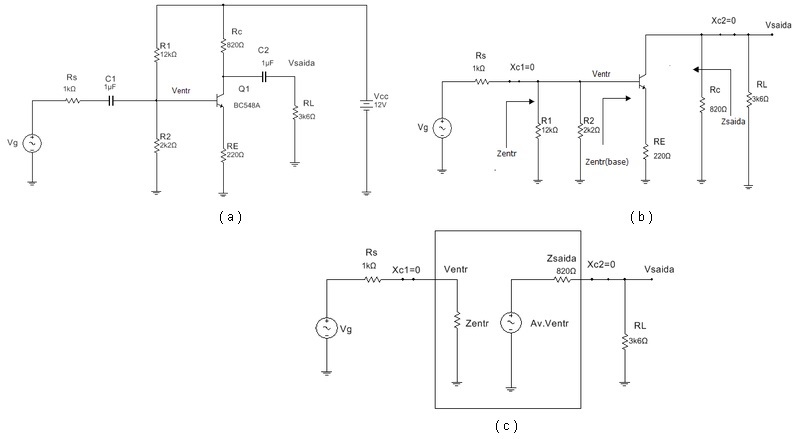
O amplificador EC da Figura 4 é essencialmente o mesmo da Figura 1, com a adição das resistências de fonte (Rs) e carga (RL). A resistência de fonte de sinal pode representar também a resistência de saída do estágio anterior e a carga pode representar a resistência de entrada do estágio seguinte.
Figura 4 - Amplificador emissor comum com realimentação - Carga finita - Resistência de fonte não nula ( a ) circuito completo ( b ) ( c ) equivalente em CA
O modelo usado para determinar a saída para uma dada entrada é o mesmo já visto na aula anterior com a diferença que o ganho é menor pois tem realimentação. As impedancias de entrada e saida são dadas por:
Zentr=R1//R2//Zentr(base) , Zentr(base)= b.(re’+ RE) e Z saida = Rc com o ganho dado por:
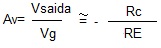
Observar que Ventr é diferente de Vg é menor pois existe uma divisão de tensão.
2. Amplificador Emissor Comum com realimentação parcial
O ganho pode ser aumentado se a resistencia efetiva de realimentação for diminuida. Na Figura 5 ao inves de um unico resistor de RE=220 
existem dois em serie RE1=100 Ohms e outro RE2=120 Ohms de forma que a soma seja igual a RE=220 Ohms como na Figura 1. Um desses resistores é desacoplado por um capacitor CE como na Figura 4a. Do ponto de vista CC as correntes e tensões não mudam, são as mesmas da Figura 1.
existem dois em serie RE1=100 Ohms e outro RE2=120 Ohms de forma que a soma seja igual a RE=220 Ohms como na Figura 1. Um desses resistores é desacoplado por um capacitor CE como na Figura 4a. Do ponto de vista CC as correntes e tensões não mudam, são as mesmas da Figura 1.Figura 5 - AEC com realimentação parcial
Os calculos são semelhantes aos dos circuitos anteriores:
Zentr=R1//R2//Zentr(base)
Zentr(base)= b.(re’+ RE1)
Zsaida = Rc
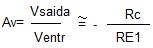
Exercicio resolvido 1
No circuito da Figura 1 calcular a saida Vsaida, se Vg=1 Vpico. Considerar b=200.
Solução: Inicialmente deve ser calculado IEQ para estimar o valor de re'
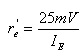
No circuito VB=(2k2.12V)/(2k2+12K)=1,86 V VE=1,86-0,7V=1,16 V portanto IE=1,16V/0,22k=5,27 mA portanto o valor do parametro re' vale:
re'=25mV/5,27mA=4,74 Ohms
A impedancia "olhando" na base vale:
Zentr(base)= b.(re'+RE)=200.(4,74 +220)=44948 W =45 k
A impedancia que a fonte Vg "enxerga" vale:
Zentr=R1//R2//Zentr(base)= 12k//2k2//45k=1,78k=1,8k
A impedancia de saida
Zsaida=Rc=820 
O valor do ganho entre a base e a saida
Av=Vsaida/Ventr= - Rc/RE= - 820/220= - 3,7
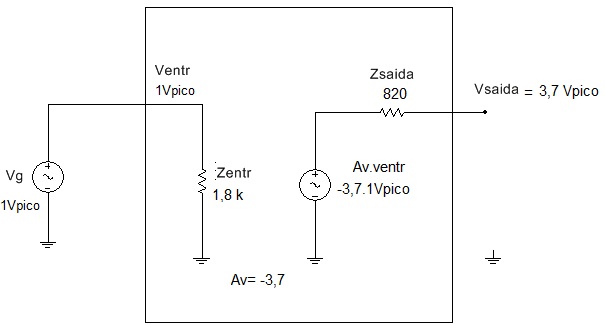
O circuito equivalente CA é mostrado na Figura 6, e como não existe resistencia de fonte (Rs=0) então Ventr=Vg= 1 Vpico
Figura 6 - AEC do exercicicio resolvido com os valores calculados
Exercicio resolvido 2
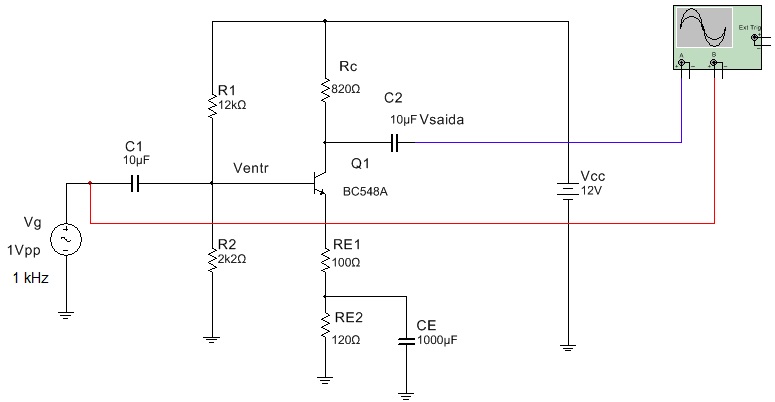
Estime o valor da tensão na saida do circuito da Figura 7.
Figura 7 - AEC com realimentação parcial - exercicio resolvido 2
Solução: Como os valores CC são os mesmos do circuito da Figura 1, o valor de de re' é o mesmo aproximadamente 4,74 Ohms.
O RE efetivo é RE1=100 Ohms, portanto o ganho da base para o coletor vale:
AV=Vsaida/Ventr= - 820/100= - 8,2 (valor exato -820/(4,74+100)= -7,8
Então Vsaida= AV. Ventr= Av.Vg= -7,8.1Vpp= -7,8 Vpp Obs: o Sinal negativo significa defasagem de 180 Graus entre Vsaida e Vg.
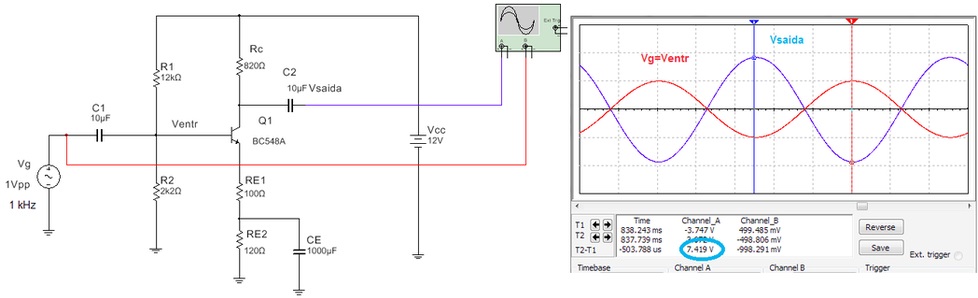
A Figura 8 mostra a medida com o osciloscopio, onde o valor medido na saida é 7,419 V.
Figura 8 - Medida da tensão de saida (Vsaida) e de entrada (ventr) para exercicio resolvido 2
Exercicio resolvido 3
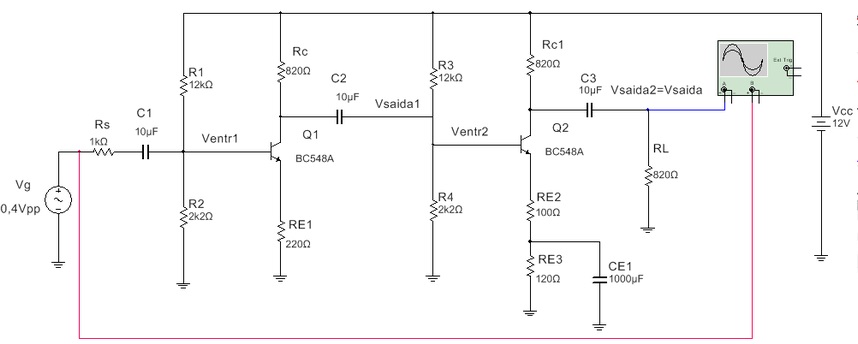
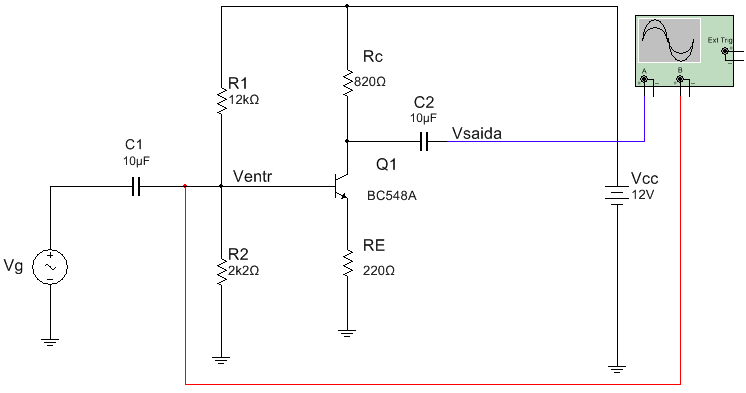
Determine a tensão na saida, Vsaida, do circuito da Figura 9. Considerar transistores iguais com b=200.
Figura 9 - Circuito para exercicio resolvido 3
Solução: O circuito tem dois estagios com resistencias de polarização iguais, o que significa que as correntes quiescente de emissor são iguais, IE1=IE2=5,27 mA, então re'=4,74 Ohms.
A impedancia de entrada do primeiro estagio vale: Zentr=R1//R2//Zentr(base1) = 12k//2k2//200.(4,74+220)=12k//2k2//44.948=1,78 k = 1,8 k
O ganho do primeiro estagio vale:
Av1=Vsaida1/Ventr1=-820/(4,74+220)=-3,64 (considerando re')
A impedancia de saida do primeiro estagio vale: Zsaida= 820 Ohms
A impedancia de entrada do segundo estagio vale: Zentr=R1//R2//Zentr(base2) = 12k//2k2//200.(4,74+100)=12k//2k2//20948= 1,7 k
O ganho do segundo estagio vale:
Av2=Vsaida2/Ventr2= - 820/(4,74+100)= - 7,8 (considerando re')
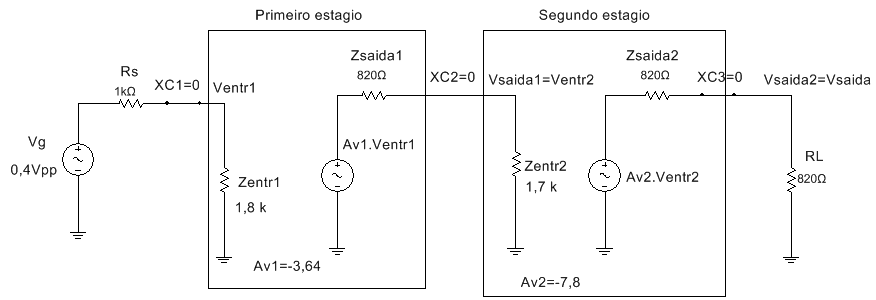
A partir das informações obtidas é desenhado o circuito equivalente CA, Figura 10.
Figura 10 - Circuito equivalente CA do circuito da Figura 9
Efetuandos os calculos da esquerda (entrada) para a direita (saida):
Ventr1=(1,8 k.0,4V)/1k+1,8k)=0,257 Vpp Tem um divisor de tensão na entrada!!!!
AV1.Ventr1= (-3,64).0,257 = - 0,935 Vpp
Ventr2=Vsaida1=(1,7k.-0,935V)/(0,82k+1,7k)= -0,63 Vpp
Av2.Ventr2= (-7,8).(-0,63V)= 4,9 Vpp
Finalmente: Vsaida2=Vsaida=(0,82k.4,9 V)/(0,82k+0,82K)= 2,45 Vpp
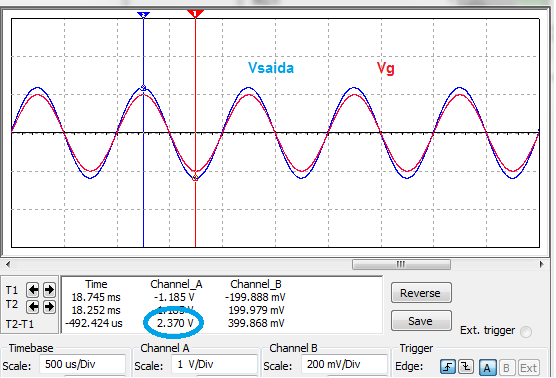
A Figura 11 mostra os valores da entrada (Vg) e saida (Vsaida) no osciloscopio. O valor medido de pico a pico resultou em 2,37 Vpp um pouco menor que o valor calculado (não esqueça é ELETRONICA). Provavelmente o valor mais correto é o lido pelo osciloscopio, pois o modelo que foi adotado para a analise é um modelo simplificado. Existem modelos mais complexos, como o modelo H, mas precisam de uma computação mais elaborada.
Figura 11 - Resultado das medidas no osciloscopio do exercicio resolvido 3
3. Experiencia: Amplificador Emissor Comum com realimentação
3.1. Abra o arquivo ExpEN1_28_AEC_com _realimentação_sem_Rs_e_RL identifique o circuito da Figura 12. Inicie a simulação medindo o valor da saida de pico a pico (Vsaidapp) anotando na tabela 1. Calcule o valor do ganho por Av=Vsaidapp(medido)/Vgpp, anote como Av(medido).
Arquivo Multisim Live
Arquivo Multisim Live
Figura 12 - Circuito para experiencia
Tabela 1 - AEC com realimentação sem carga e resistencia de fonte - Valores medidos e calculados
| Av(calculado)=-Rc/(re'+RE) | Vsaidapp(V) | Av(medido)=Vsaidapp(V)/Vgpp |
3.2. Compare os valores medidos com os calculados.
3.3. Escreva as suas conclusões.
4. Experiencia: Amplificador Emissor Comum com realimentação com resistencia de fonte e de carga
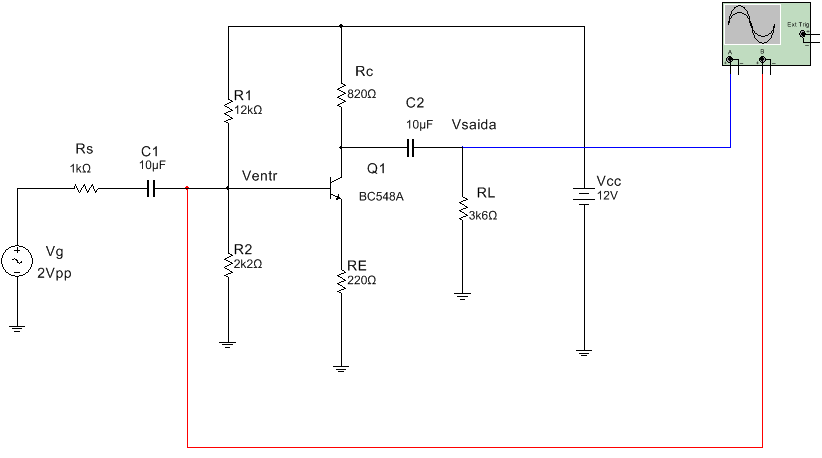
4.1. Abra o arquivo ExpEN1_29_AEC_com_realimentacao_com_Rs_e_RL (Multisim 14) identifique o circuito da Figura 13.
4.2. Inicie a simulação medindo o valor da saida de pico a pico (Vsaidapp) e do sinal na base, Ventrpp, anotando na tabela 2. Em seguida calcule o valor do ganho entre a base e a saida por Av=Vsaidapp(medido)/Ventrpp anote como Avparcial(medido).
Obs: Para facilitar a medida de Ventrpp, ligue a chave de entrada do osciloscopio em AC, desta forma será mostrado somente o sinal. Con a chave em DC aparece o sinal mais a componente de polarização (CC). Use os dois cursores para medir.
Arquivo Multisim Live
Figura 13 - AEC com realimentação com carga e resistencia de fonte
Tabela 2 - AEC com realimentação com carga e resistencia de fonte - Valores medidos e calculados
Avparcial(teorico) | AvT(teorico) | Zentr(teorico) | Vsaidapp (V) | Ventrpp(V) | Avparcial(medido) | AvT(medido) | Zentr(medido) |
4.2. Tendo medido o sinal na base, isto é, somente a parte alternada (Ventrpp), como voce sabe qual o valor de pico a pico do gerador (Vgpp) calcule a impedancia de entrada (Zentr) por:
Arquivo Multisim Live
Ventrpp é medido no osciloscopio Rs=1 k ee Vgpp=2 Vpp é dado
Anote o valor de Zentr assim determinado como Zentr(medido) na tabela 2.
4.3.Calcule o ganho total por AvT(calculado)=Vsaida/Vg. Anote na tabela 2.
4.4. Determine o ganho total por AvT=Vsaidapp/Vgpp, anote na tabela 2.
4.5. Compare os valores obtidos por medida com os valores teoricos calculados.
5. Experiencia:Amplificador Emissor Comum com realimentação parcial
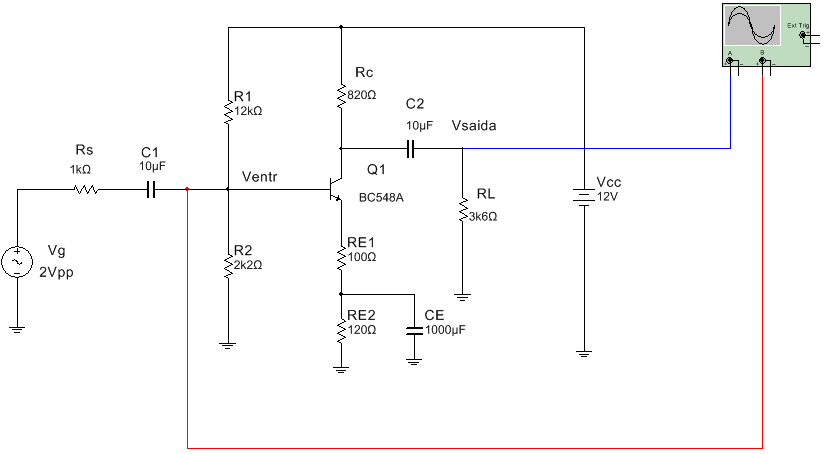
5.1. Abra o arquivo ExpEN1_30_AEC_com_realimentacao_parcial_e_com_resistencia_de_fonte_e_carga (Multisim 14) identifique o circuito da Figura 14. Inicie a simulação medindo o valor da saida de pico a pico (Vsaidapp) e do sinal na base, Ventrpp, anotando na tabela 3. Em seguida calcule o valor do ganho entre a base e a saida por Av=Vsaidapp(medido)/Ventrpp anote como Avparcial(medido).
Arquivo Multisim Live
Figura 14 - Amplificador Emissor Comum com realim entação parcial pelo emissor
Tabela 3 - AEC com realimentação parcial com carga e resistencia de fonte - Valores medidos e calculados
Avparcial(teorico) Vsaidapp/Ventrpp | AvT(teorico) Vsaidapp/Vgpp | Zentr(teorico) | Vsaidapp (V) | Ventrpp(V) | Avparcial(medido) | AvT(medido) | Zentr(medido) |
5.2. Tendo medido o sinal na base (Ventrpp), e como é conhecido o valor de pico a pico do gerador (Vgpp) calcule a impedancia de entrada (Zentr).
Anote o valor de Zentr assim determinado como Zentr(medido) na tabela 3.
5.3.Calcule o ganho total (usando as expressões) AvT(calculado)=Vsaida/Vg. Anote na tabela 3.
5.4. Determine o ganho total por AvT=Vsaidapp/Vgpp, anote na tabela 3.
5.5. Compare os valores obtidos por medida com os valores teoricos calculados.
5.6. Escreva as suas conclusões.