aulaAO014 - eletronica24h
Menu principal:
aulaAO014
Educacional > Cursos > Amplificador Operacional
Amplificador Operacional
Aula 14: Filtro Passa Baixas de Segunda Ordem
Referencia.
UTILIZANDO ELETRÔNICA COM AO, SCR, TRIAC,SCR,555 Albuquerque e Seabra
Aula 14: Filtro Passa Baixas de Segunda Ordem
Referencia.
UTILIZANDO ELETRÔNICA COM AO, SCR, TRIAC,SCR,555 Albuquerque e Seabra
1. Filtro Passa Baixas de dois pólos (Segunda Ordem)
A Figura 1 mostra um filtro ativo passa baixas de dois pólo (queda de 40dB/década), sendo assim denominado por ter dois circuitos RC. A análise matemática avançada mostra que a resposta é a mais plana possível quando o ganho de malha fechada vale 1,586 ou 4 dB, desta forma a relação entre R1 e R2 é dada por:
R2=0,586.R1, se R1 =1 k então R2=0,586K = 586 Ohms (valor comercial mais próximo 560 Ohms).
A freqüência de corte (fc) vale:
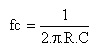
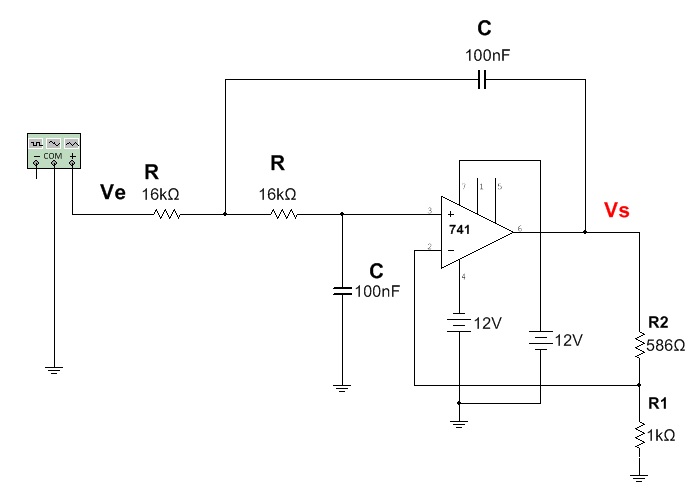
Figura 1 - Filtro Passa Baixas de segunda ordem (2 pólos)
Fonte: Multisim V. 14
1.1 Curva de Resposta em Freqüências
A Figura 2 mostra a curva de resposta em freqüências do circuito da Figura 1 com o primeiro cursor indicando o ganho no patamar (em baixas freqüências) o qual é calculado por:
G= 20.log(1+R2/R1)= 20.log1,586 = 4 dB
O segundo cursor mostra aproximadamente a freqüência de corte (100 Hz) na qual o ganho vale aproximadamente 1dB (3 dB abaixo do ganho no patamar).
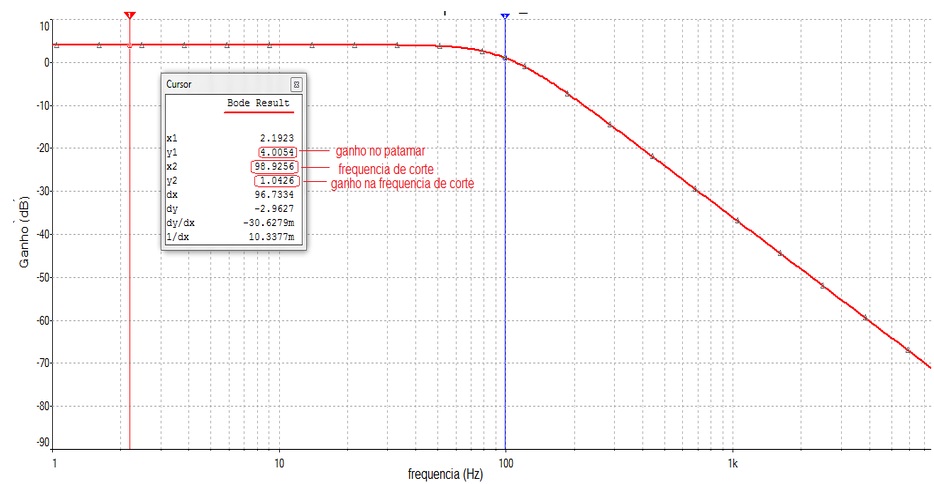
Figura 2 - Curva de resposta em freqüência do circuito da figura 1
Fonte: Multisim V. 14
O gráfico da Figura 3 mostra os dois cursores separados por uma década de frequencia (o primeiro indica 200 Hz e o segundo indica 2 kHz), a diferença nos ganhos é de 40 dB isto é, a queda do gráfico é de 40 dB/decada, maior portanto do que no circuito de primeira ordem (melhor!!!!).
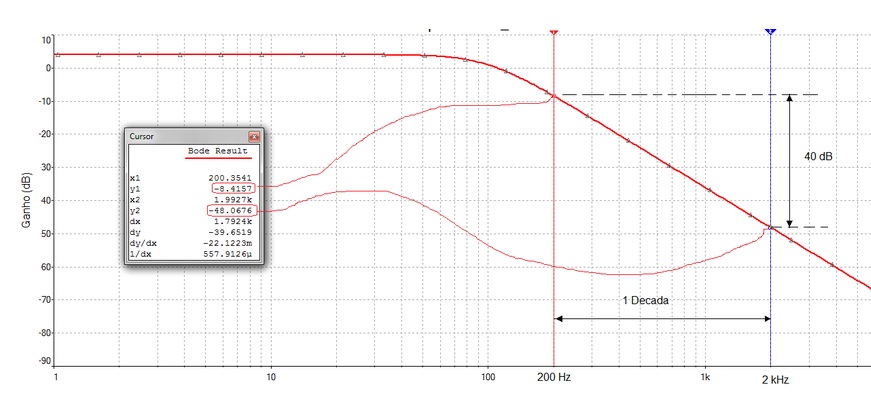
Figura 3 - Curva de resposta em frequencia com atenuação de 40 dB/decada
Fonte: Multisim V. 14
2.2 Experiência: Filtro Passa Baixas de Segunda Ordem
2.1. Abra o arquivo ExpAO_36 FPB Segunda Ordem(Multisim 14) e identifique o circuito da figura 4. Calcule a frequencia de corte e anote como fc(calculada). Inicie a simulação e use o Bode Plotter para determinar a frequencia de corte e para isso use os cursores. Anote esse valor como fc(medida).Calcule e meça o ganho para cada uma das frequencias da tabela 1.
fc(calculada)+____________ fc(medida)=_____________
Arquivo Multisim Live
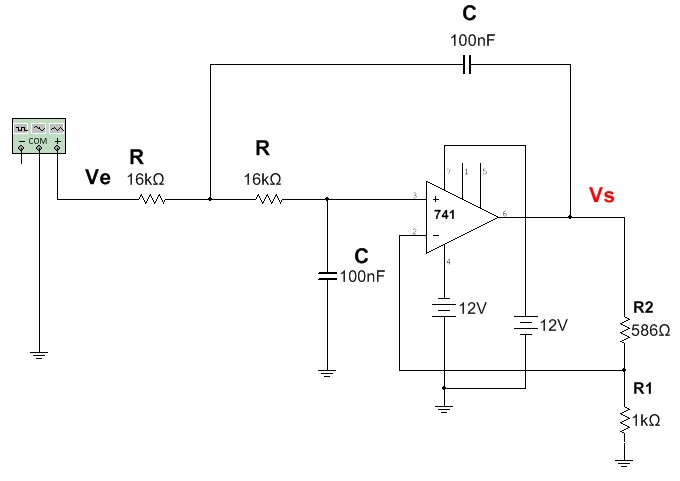
Figura 4 - FPB de segunda ordem para experiencia
Fonte: Multisim V. 14
Tabela 1 - FPB de segunda ordem - calculo e medida do ganho em diferentes freqüências
| Ganho Teórico | Ganho Simulado | |||||
fc | 10.fc | 100.fc | fc | 10.fc | 100.fc | |
| Valor do ganho (dB) | ||||||
3.2 Com o gerador de funções em onda senoidal e amplitude de 1 Vpp (0,5 Vpico) meça o valor da tensão de saída de pico a pico para as freqüências da Tabela 2. Anote também a defasagem entre Vs e Ve.
Tabela 2 - FPB de segunda ordem - medindo e calculando a amplitude da saída em diferentes frequencias
Teórico | Simulado | |||
| freqüência | fc | 10.fc | fc | 10.fc |
Vspp | ||||
Defasagem | ||||
3.3 Para cada valor de freqüência da tabela 3, meça o valor da saída de pico a pico (Vspp), em seguida efetue os cálculos de Vspp/Vepp, e 20.log(Vspp/Vepp).
Com os dados da tabela levante o gráfico do ganho (20.logVspp/Vepp ) em função da freqüência. Use papel monolog, sendo na vertical escala de ganho linear (dB) e na horizontal escala de freqüências logarítmica .
Considerar Ve=1 Vpp.
Considerar Ve=1 Vpp.
Tabela 3 - FPB de segunda ordem - Medindo o ganho para diferentes freqüências - curva de resposta em frequencia
f(Hz) | 100 | 500 | 1 k | 1,5 k | 2 k | 5 k | 10 k | 15 k | 20 k | 30k |
Vspp | ||||||||||
Vspp/1V | ||||||||||
20.log(Vspp/1) |
2.4 Escreva as suas conclusões
