aulaCA004 - eletronica24h
Menu principal:
aulaCA004
Educacional > Cursos > Eletricidade em CA
Analise de Circuitos em Corrente Alternada
Aula04: Indutor em CC - Indutor em CA - Reatancia indutiva
Bibliografia
Aula04: Indutor em CC - Indutor em CA - Reatancia indutiva
Bibliografia
Analise de Circuitos em Corrente Alternada - Editora Erica
1 O Indutor
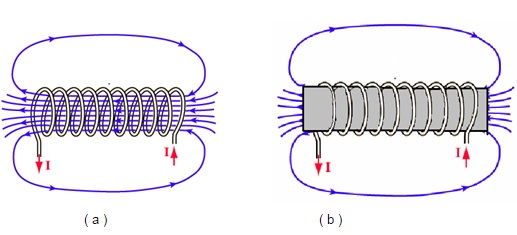
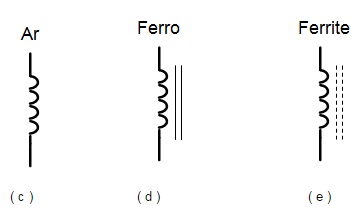
O indutor é outro componente basico da eletricidade/eletronica. É essencialmente semelhante ao solenoide, Figura 1, com menores dimensões.

( d )
Figura 1 - Indutor ( a ) nucleo de ar ( b ) nucleo de ferro ou ferrite simbolos ( c ) nucleo de ar ( d ) nucleo de ferro ( e ) nucleo de ferrite ( d ) aspecto fisico
2 Indutor em CC
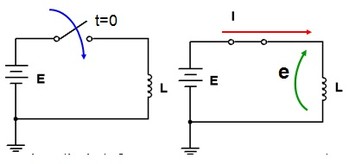
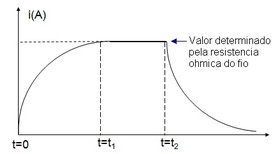
No circuito da Figura 2 a chave é fechada no instante t=0. A partir de t=0 a corrente começa a aumentar, e ao passar pela espiras origina um campo magnetico cujas linhas de campo cortam as espiras subsequentes induzindo nelas uma fem autoinduzida que se opõe ao aumento de corrente. Após um tempo t1 a corrente atinge I imposta pelas resistências ôhmicas.
( a )



( b ) ( c )
Figura 2 - Comportamento do indutor em CC ( a ) chave é fechada ( b ) chave é aberta ( c ) comportamento grafico
Figura 2 - Comportamento do indutor em CC ( a ) chave é fechada ( b ) chave é aberta ( c ) comportamento grafico
Use o Arquivo Multisim para observar o mesmo grafico da Figura 2
Arquivo Multisim - Indutor em CC
Conclusões
- Um indutor se opõe à variação da corrente;
- Em um indutor a corrente está atrasada em relação a tensão. (a tensão é máxima e a corrente ainda está crescendo).
Indutância (L)
Se um núcleo de ferro for colocado na bobina a oposição oferecida pela bobina será maior, isto porque a indutância (L) será maior.
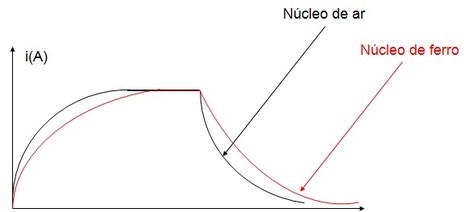
Figura 3 - Comportamento da corrente com indutor de nucleo de ar e nucleo de ferro
A indutância (L) de uma bobina é uma propriedade que tem a bobina para armazenar energia no campo magnético. É a medida da capacidade que tem uma bobina de armazenar energia. A sua unidade é o Henry (H). A indutância depende das dimensões da bobina e do material do nucleo.
A Figura 4b mostra a equação basica de um indutor
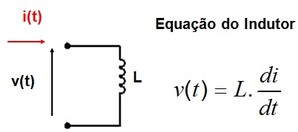
Figura 4 - Relação entre corrente, tensão e indutancia em um indutor
Qual o significado da equação? Se a corrente for constante não haverá tensão induzida (v=0) (A derivada é nula).
di e dt é uma variação (D) muito pequena, ou como dizem os matematicos, infinitesimal.
di/dt é a derivada da corrente em relação ao tempo
3 Indutor ideal em corrente alternada senoidal
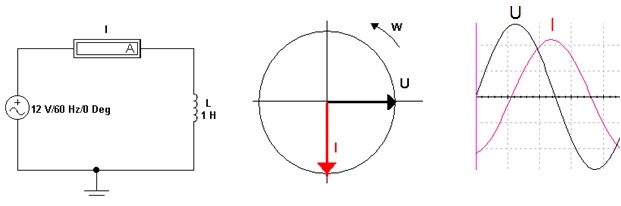
Se a um indutor ideal (resistência ôhmica nula) for aplicada uma tensão senoidal, a corrente resultante será senoidal e atrasada de 90o em relação à tensão aplicada.
( a ) ( b ) ( c )
Figura 5 - Indutor ideal em CA ( a ) circuito ( b ) Diagrama Fasorial ( c ) Formas de onda da tensão e corrente
Neste caso v(t)=Vp.sen(w.t) i(t)=Ip.sen(w.t - 900) ou
Forma polar
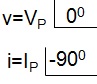
Rorma cartesiana
v=Vp (V) e i=- jIp (A)
Reatância Indutiva
Como vimos um indutor se opõe à variação de uma corrente. A medida desta oposição é dada pela sua reatância indutiva (XL), sendo calculada por:
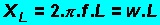
Com L especificado em Henries (H), f em Hertz (Hz), XL em ohms (W).
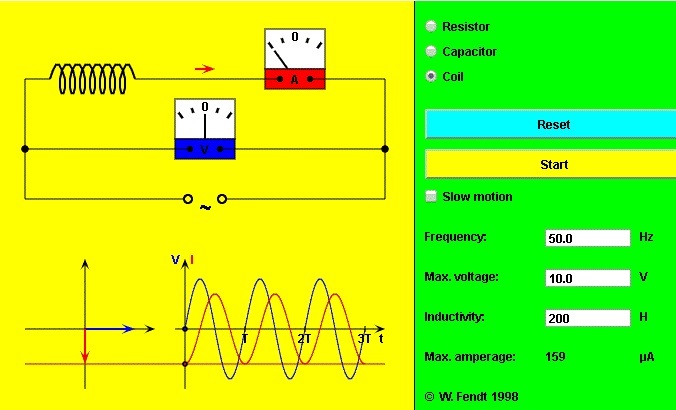
A seguir uma aplicação Java que mostra o Diagrama Fasorial em um circuito puramente indutivo. Selecione Coil (Bobina) para ver o Diagrama Fasorial e as formas de onda de tensão e corrente.
Exercício1: Uma bobina tem 0,1 H de indutância, sendo ligada a uma tensão de 110 V, 60 Hz. Determinar:
a) Reatância da bobina (XL) b ) Valor da corrente no circuito ( I )
Solução:
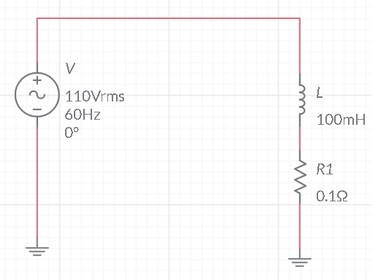
Figura 6 - Circuito para exercicio 1
Obs: A imagem da Figura 6 mostra uma resistencia de 0,1 Ohm necessaria para a simulação do Multisim. Observe que o seu valor é muito menorque a reatancia, portanto o resultado é muito proximo ao valor sem a resistencia.
a) XL = 2.p.60.0,1 = 37,7 Ohms
b) I = V / XL = 110 / 37,7 = 2,9 A
Primeira Lei de OHM para indutor ideal
Considerando que a tensão tem fase zero, a corrente estará atrasada de 900 em relação a tensão, valendo a primeira lei de OHM:
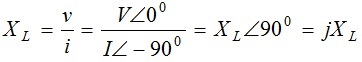
Desta forma podemos representar a reatância indutiva por:

Potencia em um Indutor Ideal
O gráfico da potencia instantânea é obtido fazendo-se: p(t)=v(t).i(t) p(t) é a potencia instantanea
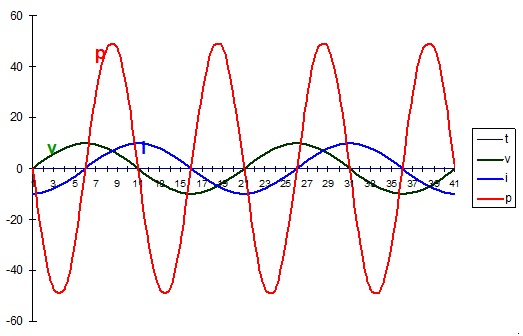
Figura 7 - Graficos da tensão em função do tempo, v(t), corrente em função do tempo, i(t) e potencia em função do tempo, p(t) em um indutor ideal
Conclusões:
- Observando o gráfico da potencia instantânea verificamos que o seu valor médio é zero, significando que em um circuito puramnete indutivo não há consumo (dissipação) de potencia;
- Quando a potencia é positiva, significa que o o indutor está recebendo. Energia do gerador e armazenando-a na forma de campo magnético;
- Quando a potencia é negativa , significa que o o indutor está se comportando. Como gerador, devolvendo a energia armazenada.
Potencia Ativa
Chamamos de potencia ativa (P) ou potencia real a potencia que é transformada em energia útil, sendo calculada por:
P=VEF.IEF.cos f (W)
VEF tensão eficaz aplicada no indutor (V)
IEF corrente eficaz aplicada no indutor (A)
cosf é o fator de potencia do circuito, um parametro muito importante na industria e deve ser controlado com valor maior ou igual a 0,92
f é o angulo de defasagem entre a tensão e a corrente, neste caso 900 e portanto P=0 como esperado.
4 Experiencia: Indutor em CA
4.1 Abra o arquivo ExpCA08_Indutor em Corrente Alternada - medida da reatancia (Multisim 14) e identifique o circuito da figura 8. Inicie a simulação medindo a tensão no indutor e a corrente. Calcule a relação entre V e I. anote na tabela 1. Compare esse valor com o calculado. Repita o procedimento para f=180 Hz.
Arquivo Multisim Live - Indutor em CA

Figura 8 - Medindo a reatancia (XL)
Tabela 1 - Indutor em CA - medida da reatancia indutiva
| f= 60 Hz | f= 180 Hz | ||||||
XL=2. .f.L .f.L(Ohms) | V (V) | I(A) | XL=V/I (Ohms) | XL=2.  .f.L .f.L(Ohms) | V (V) | I(A) | XL=V/I (Ohms) |
4.2 Abra o arquivo ExpCA09_ Indutor em Corrente Alternada - medida da defasagem (Multisim 14) e identifique o circuito da Figura 9. Inicie a simulação. Meça a defasagem, no tempo, entre a tensão (v1) e a a corrente (tensão em R). atraves de uma regra de tres transforme a defasagem no tempo para graus. Comparae com a esperada. Observe que o valor de R é muito menor que XL, isto é, o circuito pode ser considerado praticamente indutivo.
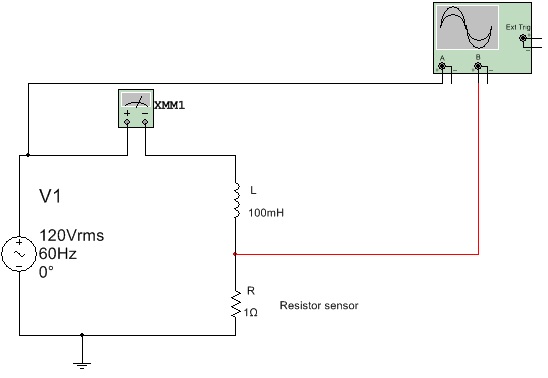
Arquivo Multisim live - Medindo defasagem entre V e I em um indutor

Figura 9 - Circuito para experiencia - medindo a defasagem entre tensão e corrente
Tabela 2 - Medindo a defasagem entre a corrente e tensão em um indutor
| Defasagem no tempo (ms) | Defasagem em graus |
4.3. Escreva as suas conclusões.