aulaCA005 - eletronica24h
Menu principal:
aulaCA005
Educacional > Cursos > Eletricidade em CA
Analise de Circuitos em Corrente Alternada
Aula05: Circuito RL serie - Triangulo das tensões, impedancias e potencia - Impedancia - Fator de potencia
Bibliografia
Analise de Circuitos em Corrente Alternada - Editora Erica
1. Circuito RL Série
Na prática um indutor apresenta uma resistência, e além disso podemos ter resistores em série com o indutor, neste caso a corrente continuará atrasada em relação à tensão mas de um angulo menor do que 90º. A Figura 1 mostra o circuito e o diagrama fasorial. Observe que a fase da corrente foi considerada arbitrariamente igual a zero. Todos os outros fasores estarão "amarrados" a isso. A oposição total é devido a resistencia (R) e a reatancia indutiva (XL) sendo chamada de impedancia (Z). No circuito da figura 1, L representa um indutor ideal a sua resistencia está incorporada a outras resistencias sendo representada por R.
Se a fase da corrente for zero, a tensão na resistencia estará em fase com a corrente. Por outro lado a tensão no indutor esta atrasada de 900 em relação a corrente que é a mesma no indutor e na resistencia.
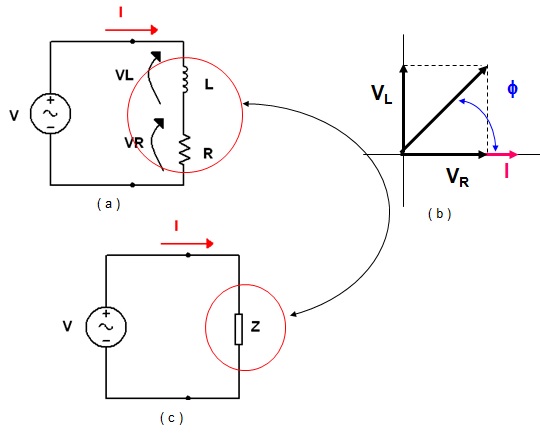
Figura 1 - ( a ) Circuito RL serie ( b ) Diagrama Fasorial ( c) Impedancia (equivalente)
Impedância indutiva (ZL)
A impedancia, Z, é a combinação dos efeitos da resistencia, R, e da reatancia indutiva, (XL).
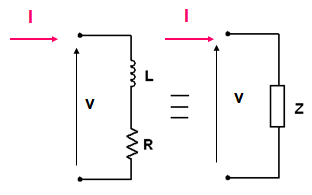
Figura 2 - Impedancia Indutiva
As tres grandezas são complexas (tem modulo e fase) e estão relacionadas entre si pela primeira lei de Ohm, Figura 3:
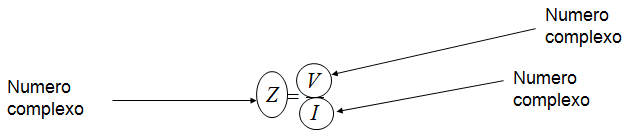
Figura 3 - Relação entre V, I e Z em um circuito RL serie
Relações no circuito RL serie - Triangulo das Tensões
A Figura 4 , mostra o triangulo das tensões e as principais grandezas (I,V, XL e Z).

Figura 4 - Relações no circuito RL serie
V=VR+VL, soma vetorial, que dividindo por I resulta:

Que é a impedancia na forma cartesiana
Impedância na forma polar - Triangulo das Impedancias
Se no triangulo das tensões cada um dos lados for dividido por I, o triangulo resultante será chamado de triangulo das impedancias, não mudando os angulos. Observe que a defasagem entre a corrente e a tensão total, f, é agora o angulo entre a impedancia (Z) e a resistencia (R) e é o mesmo da Figura 4.
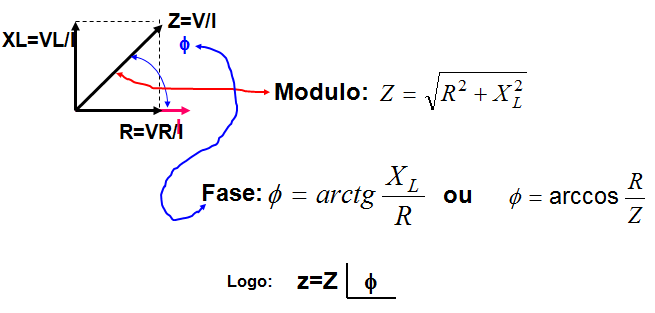
Figura 5 - Obtendo a impedancia na forma complexa polar
O exemplo a seguir é fundamental para a analise de circuitos em CA. Acompanhe a solução e depois tente resolver sem ver a solução.
Exercicio Resolvido 1: Dado o circuito pedem-se:
a) Valor da impedância (Z) e sua representação nas formas polar e cartesiana
b) Valor da indutância (L)
c) Valor da corrente (I) e sua representação nas formas polar e cartesiana
d) Valor de VR e VL e suas representações na forma polar e trigonométrica
e) Diagrama fasorial
Solução:
a) A impedância na forma cartesiana é Z=30+j40 (Ω) obtido direto do circuito, lembre-se é serie (soma).
Na forma polar.
Para obter a impedancia na forma polar, pense na impedancia como um numero complexo com parte real 30 e parte imaginaria 40. Represente-o no sistema de eixos cartesianos, aparece um triangulo retangulo de lados conhecidos.
Para obter a impedancia na forma polar, pense na impedancia como um numero complexo com parte real 30 e parte imaginaria 40. Represente-o no sistema de eixos cartesianos, aparece um triangulo retangulo de lados conhecidos.
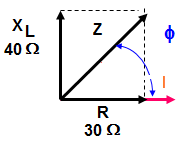
Do retangulo das impedancia obtemos:
O modulo de Z A fase de Z Impedancia Z na forma polar
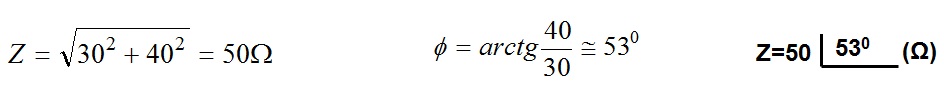
b) Pela reatância indutiva obtém-se L

c) Corrente no circuito
Na forma polar
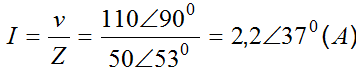
Na forma cartesiana
I =2,2.cos370 + j2,2.sen370 = 1,75 +j1,32 (A)
d) Tensões na resistencia (VR) e indutor (VL) nas formas complexas e trigonometrica.
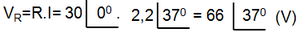 | logo |  |
 | logo |  |
Tensão em L na forma polar

Tensão em R na forma polar
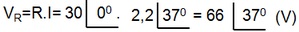
Tensão em R e L na forma trigonometrica
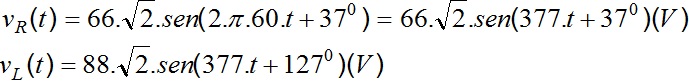
e) Diagrama Fasorial

As fases das tensões e da corrente são referenciadas na origem e podem mudar. O que não muda é a defasagem entre a tensão total e a corrente.
Para verificar a solução use o Multisim Live ou
Arquivo Multisim Live - Exercicio Resolvido1
Calculador de https://www.walter-fendt.de. Se usar esse calculador, começe mudando a tensão (default 12V), para 110V e frequencia (default 50Hz) para 60Hz., clique em Replace. Depois mude o valor da resistencia (padrão 1000)., para 30 Ohms, clique em Replace. Selecione Add(inserie) ). Selecione o Componente que deseja ligar em serie, Indutor... Clique Replace. Mude o valor para 0.106H. Os resultados aparecem na tabela abaixo e esquerda.
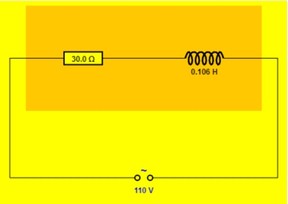
Potencia em um circuito RL serie
Para a analise da potencia seja o triangulo de tensões do diagrama fasorial da Figura 1b. Multipliquemos cada um dos lados por I, resultará o triangulo de potencia, Figura 6.
Triangulo das tensões | Triangulo das potencias | |
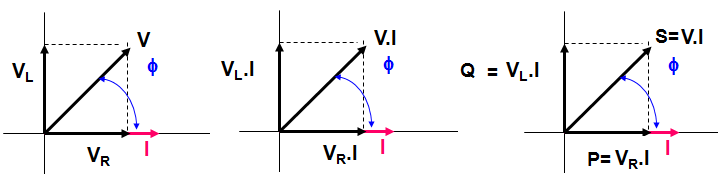 | ||
| ( a ) ( b ) | ||
| Figura 6 - Obtendo o triangulo das potencias a partir do triangulo dsa tensões | ||
Q=PR=VL.I=V.I.senf é a potencia reativa do circuito (VARi), obs: no livro Analise de Circuitos em CA é a potencia reativa = PR | ||
S=PAP=V.I é a potencia aparente do circuito (VA), obs: no livro Analise de Circuitos em CA potencia aparente é PAP | ||
P=VR.I=V.I.cosf é a potência real ou ativa do circuito (W) | ||
Qual a relação entre essas potencias? Basta olhar o triangulo das potencias que obtem-se:
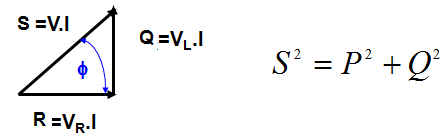
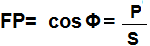
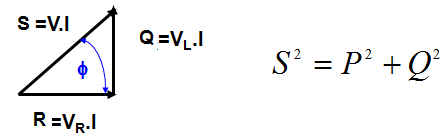
S=potencia aparente em VA
P=Potencia real ou ativa em W
P=Potencia real ou ativa em W
Q=Potencia reativa em VARi
Fator de potencia
O Fator de potencia como o nome diz, é a relação entre a potencia ativa (W) e a potencia aparente (VA):
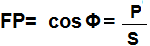
O FP é uma medida do aproveitamento da energia fornecida pelo gerador ao circuito. Por exemplo, em um circuito puramente resistivo, o FP=1, o que significa? Que toda a energia fornecida pelo gerador é transformada, no caso em calor. No caso de um indutor ideal, FP=0, significando que não existe energia transformada.
Resumindo
Potencia util: P= S.cosΦ=V.I.cos f (W) é a potencia medida por um Wattimetro
Potencia aparente: S=V.I (VA)
Potencia reativa: Q=V.I.sen f
Potencia aparente: S=V.I (VA)
Potencia reativa: Q=V.I.sen f
Exercicio Resolvido 2
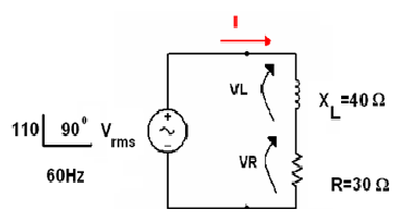
No circuito do exercicio Resolvido 1, calcule:
a) Potencia real (util) P
a) Potencia real (util) P
b) Potencia aparente (S)
c) Potencia reativa Q

Solução:
a) Ja foram calculados I=2,2 A f=53 graus logo cos 53= 0,6=F.P
P=110V.2,2.0,6=145 W
P=110V.2,2.0,6=145 W
b) S=110V.2,2A= 242 VA
c) Q=V.I.senf= 110V.2,2A.0,8=193 VARI
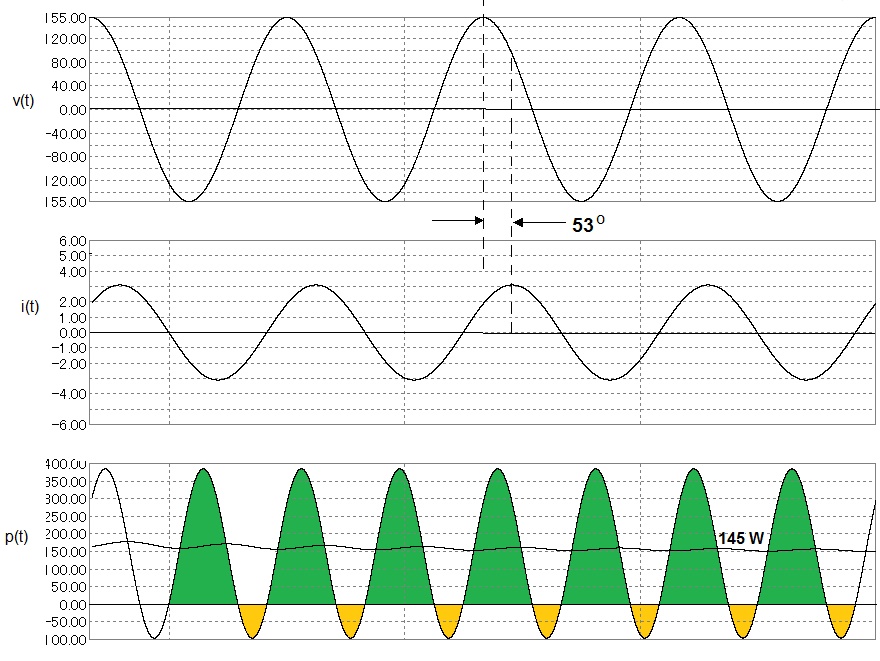
Os graficos mostram as formas de onda da tensão, v(t), da corrente, i(t), e da potencia instantanea, p(t)=v(t).i(t).

No grafico da potencia instantanea, a area verde esta associada a energia util, transformada, a area amarela esta associada a energia reativa.
O valor medio dessa forma de onda é a potencia media (145 W).
O valor medio dessa forma de onda é a potencia media (145 W).
RESUMO
Carga Puramente Resistiva
Como Φ=0 portanto cos Φ=1 a carga aproveita toda a energia fornecida pelo gerador.
Carga Puramente Indutiva
Como Φ=90 portanto cos Φ=0 não há potencia ativa, a carga troca energia entre o gerador e a carga.
Carga Indutiva e Resistiva
Como 0<Φ<90 portanto 0<cos Φ<1 há potencia ativa, a carga aproveita apenas uma parte da energia fornecida.
Exercicios resolvidos 3
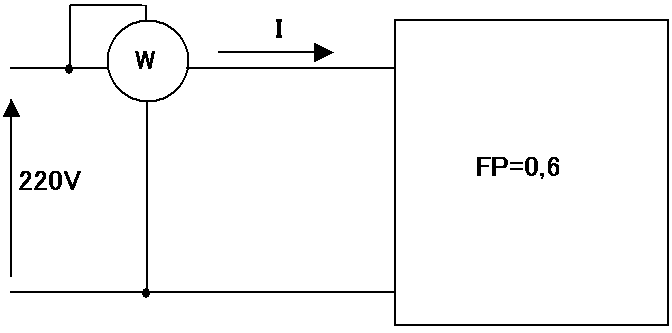
A potencia consumida (ativa) por uma instalação elétrica é de 2400 W. Se a tensão de alimentação é 220 V, calcular a potencia
aparente e corrente quando:
a) FP=0,6 b) FP=0,9
Solução:
a) A situação é mostrada na Figura 7.

Figura 7 - Exercicio resolvido - FP=0,6
Solução
A potencia util é a potencia medida no wattimetro está relacionada com a corrente, tensão e FP
2400=220.I1.0,6 I1=18,18 A
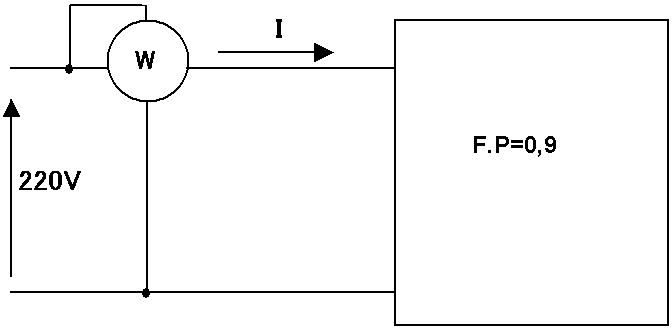
b) O que acontece se o FP aumentar, por exemplo ligando em paralelo um capacitor de valor adequado (veremos em outra aula sobre essa questão).

Figura 8 - Exercicio resolvido - FP=0,9
Em outras aulas estudaremos o capacitor e a correção do FP, por enquanto considere que o mesmo circuito (pode ser um motor operando sob determinada carga) consome a mesma potencia util, isto é, 2400 W. O que muda? Vejamos:
2400=220.I2.0,9 I2=12,12 A
Então o aumento do FP diminui a corrente para a mesma carga funcionando nas mesmas condições.enci
2. Experiencia: Circuito RL serie - Medida das tensões e corrente - Medida da potencia e do FP
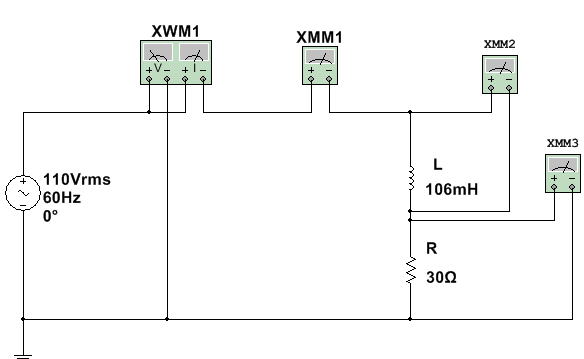
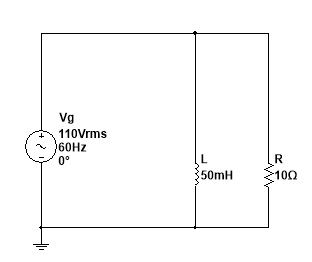
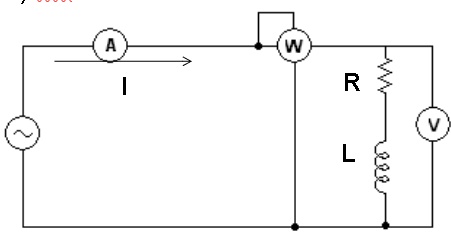
2.1. Abra o arquivo ExpCA10_RL_serie_medida_da_tensão_corrente_e_potencia (Multisim 14) e identifique o circuito da figura 9. Inicie a simulação e meça as tensões,a corrente a potencia ativa o fator de potencia e a defasagem entre a tensão total e a corrente. Anote os valores medidos na tabela 1.
Arquivo Multisim Live - CircuitoRL medida da corrente

Figura 9 - Circuito para experiencia - Circuito RL serie
| Valores calculados | Valores medidos | ||||||||||
| VL(V) | VR(V) | I(A) | P(W) | F.P | 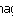 (graus) (graus) | VL(V) | VR(V) | I(A) | P(W) | F.P | 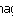 (graus) (graus) |
2.2. Escreva as suas conclusões.



3. Exercicios Propostos
3.1. Em um circuito RL a tensão total é dada por v(t)=50.sen(377.t + 500)(V) e a corrente total por i(t)=10.sen(377.t - 200)(A). Determinar os valores de R e L.
3.2. Para o circuito pedem-se:
a) Valor da corrente I
b) Potência real, P
c) Potência aparente, (PAp=S)
d) Potencia reativa, (PR=Q)
a) Valor da corrente I
b) Potência real, P
c) Potência aparente, (PAp=S)
d) Potencia reativa, (PR=Q)
e) Fator de Potencia (cosseno fi)
f) Desenhar o DF

Figura 10 - Circuito para exercicio Proposto 3.2

Figura 10 - Circuito para exercicio Proposto 3.2
3.3. No circuito a tensão alternada senoidal (80fase45graus) alimenta duas impedâncias cujos valores são dados. Calcular valor da tensão V1 em volts representado na forma polar.

Figura 11 - Circuito para exercicio Proposto 3.3
3.4 A expressão em função do tempo de uma tensão é v(t)= 30.sen(377.t + 3)(V) sendo aplicada a um circuito e resultando na corrente i(t)=10.sen(377.t + 6)(A). Pedem-se:
a) Qual o F.P do circuito?
b) Qual a expressão na forma complexa cartesiana da impedância do circuito?
3.5 No circuito v(t)=100.sen(377.t + 500)(V) e i(t)=5.sen(377.t - 200)(A).
Determinar os valores de R e L.

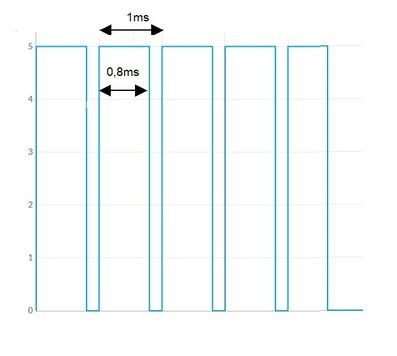
3.6 Calcule o valor médio e o ciclo de trabalho da tensão em cada caso


3.7 Determinar a impedância do circuito e todas as correntes (IG, IR e IL).

3.8 A potencia consumida (ativa) por uma instalação elétrica é de 2400 W. Se a tensão de alimentação é 220 V, calcular a potencia aparente e corrente quando:
a) FP=0,6 b) FP=0,9
R: a) I=18,18 A b) I=12,12 A
3.9 Um circuito consome 10 A, quando ligado em 220 V. Um wattímetro ligado ao circuito indica 2000 W. Calcular o fator de potencia do circuito e a potencia reativa.
R: FP=0,91 Q= 916 VARI
3.10 No circuito a leitura dos instrumentos é V=220 V, I=55 A e P=10 kW.
Calcular: a ) Impedância do circuito b) Valor da resistência e indutância (f=60Hz) c) Potencia aparente e reativa d ) FP

R: a) Z= 4 Ohms b) R= 3,3 Ohms XL=2,26 Ohms L=6 mH c) S=12,1 kVA Q= 6,8 kVARI
