aulaCA006 - eletronica24h
Menu principal:
aulaCA006
Educacional > Cursos > Eletricidade em CA
Analise de Circuitos em Corrente Alternada
Aula06: Capacitor em Corrente Continua - Carga e Descarga
Bibliografia
Analise de Circuitos em Corrente Alternada - Editora Erica
Aula06: Capacitor em Corrente Continua - Carga e Descarga
Bibliografia
Analise de Circuitos em Corrente Alternada - Editora Erica
1 Capacitores
1.1 Introdução
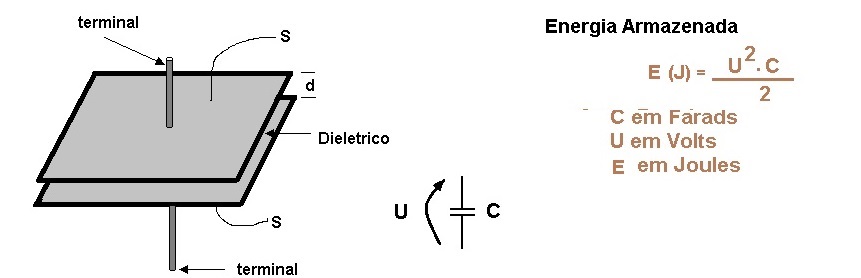
( a ) ( b )
Figura 1: Capacitor ( a ) aspectos construtivo ( b ) Símbolo
Capacitância (C)
É a medida da capacidade que tem o dispositivo de armazenar cargas elétricas. O seu valor é especificado em Farads (F) e depende das dimensões (S, d) e do material de que é feito o dielétrico (isolante que separa as duas placas).
A capacitância depende da área das placas e da espessura do dielétrico. No caso de um capacitor de placas planas e paralelas a capacitância é dada por:
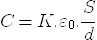
onde eo é a permissividade dielétrica do vácuo e K é a constante dielétrica do material, S a área da placas e da distancia entre uma placa e d a espessura do dielétrico. Em função do tipo de dielétrico temos os diversos tipos de capacitores.
1.2 Capacitor ligado a uma tensão CC
Ao ser ligado a uma tensão CC, devido à tensão aplicada elétrons se deslocarão de uma placa para a outra enquanto houver d.d.p, Figura 2. Quando a tensão entre as placas for igual à tensão da fonte cessará o movimento de elétrons. Nessas condições dizemos que o capacitor estará carregado, o capacitor ficará carregado com uma carga Q cujo valor é função da tensão aplicada e de uma característica do capacitor chamada de capacitância (C) sendo dada por:
Q = V. C
onde Q é especificado em Coulombs (C) V em Volts (V) e C é a capacitância especificada em Farads (F).
Desta forma se for aplicado uma tensão de 1 V a um capacitor de capacitância de 1 F a carga adquirida será de 1 C, isto é, em uma placa estarão faltando 6,25.1018 eletrons e na outra placa terá esse mesmo numero de eletrons.
Exemplo: se C=470 mF e V=50 V qual a carga armazenada?
Q=470.10-6.10= 10-3C=4,7 mC
A energia armazenada é:
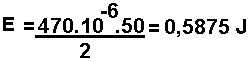
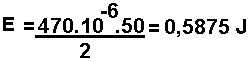
A Figura 2 mostra como o capacitor se carrega, ligando diretamente o capacitor a fonte.
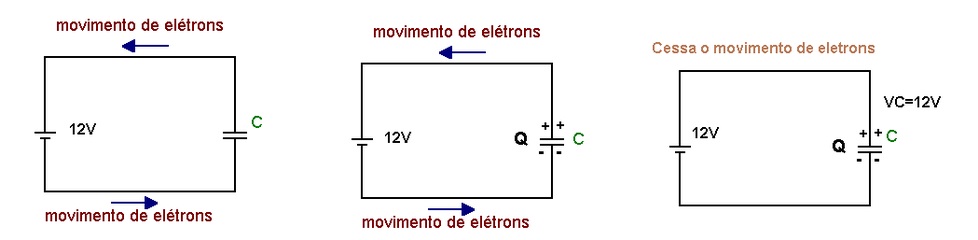
( a ) ( b ) ( c )
Figura 2 - ( a ) Capacitor inicialmente descarregado, Vc=0 ( b ) Começa o fluxo de elétrons (corrente) de uma placa para a outra ( c ) Cessa o fluxo de eletrons pois a tensão em C é igual à tensão da fonte
Devido à DDP (tensão) aplicada entre as placas os elétrons se deslocam da placa superior em direção da placa inferior e passando pela fonte. Quando a tensão entre as duas placas for igual à tensão da fonte cessa o fluxo de elétrons. Na prática indicamos o sentido da corrente no sentido contrário (corrente convencional).
Observe que não existe corrente através do capacitor, mas pelo circuito externo.
1.3 Carga do capacitor ligado a uma resistencia
Constante de Tempo
Uma medida da velocidade de carga (ou de descarga) é dada pela constante de tempo do circuito definida como sendo:
t(tau ) = R. C sendo t em segundos (s) , R em ohms (W) e C e faradas (F).
Fisicamente, uma constante de tempo é definido como sendo o tempo que a tensão leva para ir de zero até 63% da tensão da fonte (0,63.VCC).
Observe na Figura 3b que a segunda lei de Kirchhoff é verificada em qualquer instante, isto é:
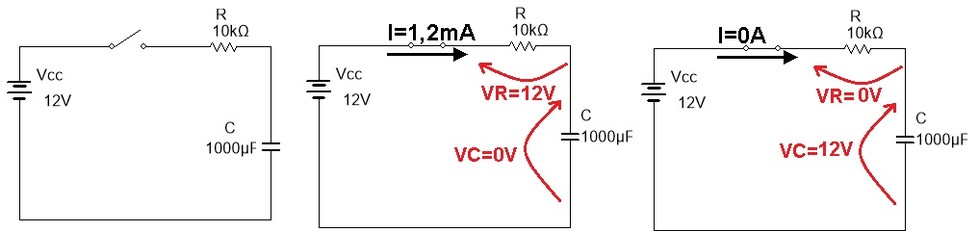
No circuito, a chave é fechada em t=0, considerando que o capacitor está inicialmente descarregado, Vc(0)=0.
( a ) ( b ) ( c )
Figura 3 - Carga do capacitor C atraves de uma resistencia R ( a ) Instante antes de ligar a chave b) Instante apos ligar a chave c) capacitor totalmente carregado
Arquivo Multisim Live
De acordo com a 2a Lei de Kirchhoff: Vcc=VR + VC (em qualquer instante)
Em t=0 VR(0) + VC(0)=VCC como Vc(0)=0 então VR(0)=VCC=12V
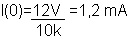
Então C começa a carregar, Vc começa a aumentar e VR começa a diminuir e portanto I começa a diminuir. Depois de um determinado tempo (que depende de C e R), o capacitor estará praticamente carregado. O gráfico da tensão em função do tempo da tensão em C e mostrado na figura 4a e o da tensão em R é mostrado na figura 4b sendo do tipo de uma função chamada de exponencial.
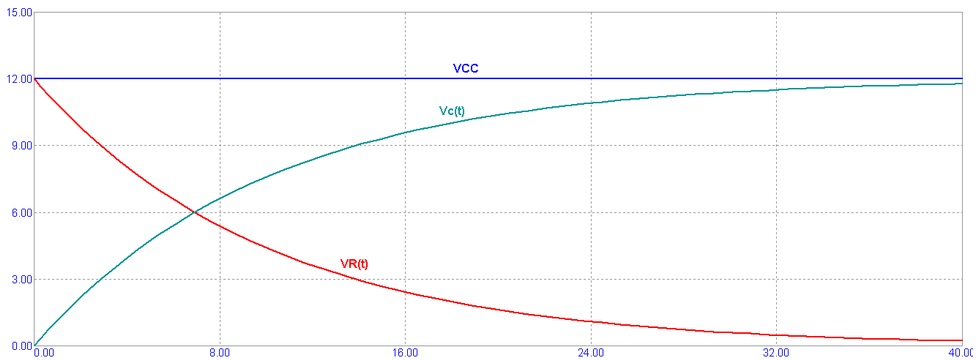
Figura 4 - Grafico da tensão em função do tempo de Vc(t) e VR(t)
A equação que descreve matematicamente a carga de um capacitor é:
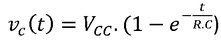
e a expressão da tensão na resistencia é:
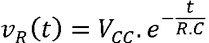
onde R.C é a constante de tempo
Por exemplo, se t=0 se substituirmos na equação da tensão em C resultará zero e na equação da tensão na resistencia resultará VCC.
Se t= R.C = 10 k. 1000 m F = 10 s substituindo na equação de vc(t) resulta v(10s)= 7,56 V.
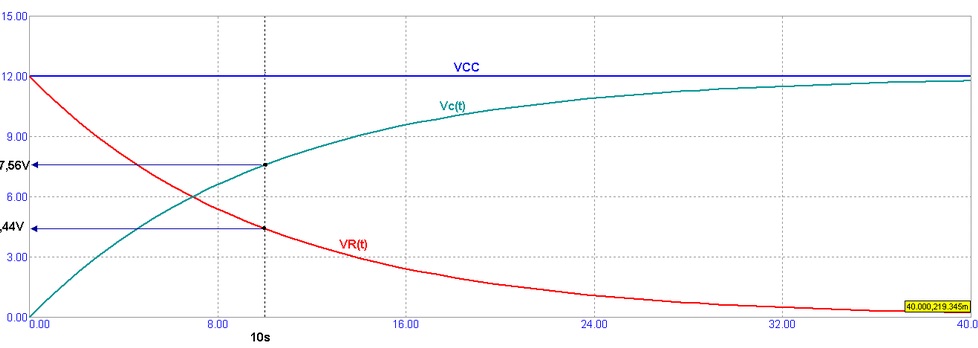Figura 5 - Grafico indicando os valores das tensões no capacitor e resistor apos 10s
Teoricamente, de acordo com a equação, a carga total só acontecerá após um tempo infinito, mas na prática bastam 4 constantes de tempo para considerarmos o capacitor totalmente carregado (Para 4 constantes de tempo a tensão atingirá aproximadamente 0,98.Vcc ).
O comportamento da corrente no circuito em função do tempo é:
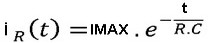
Onde IMax é Vcc/R (1,2 mA no exemplo da figura 3)
Observe que a corrente é máxima quando a chave é fechada, isso é muito importante pois mostra que um capacitor que está inicialmente descarregado se comporta como um "curto circuito".
Conclusões:
- Do ponto de vista físico não existe movimento de cargas (corrente) através do capacitor (as cargas se movimentam no circuito externo);
• A corrente no capacitor está adiantada em relação à tensão (I é máximo Vc=0);
• O tempo de carga depende da constante de tempo do circuito definida como sendo t =R.C, sendo C em Farads (F) R em Ohms (W) t em segundos(s);
• Na pratica bastam 4 constantes de tempo para carregar um capacitor.
1.3 Descarga do capacitor
Considerando o capacitor totalmente carregado com Vc=Vcc=12 V R=10 k e C=1000 mF. Como fazer para descarregar o capacitor ? Deve haver um condutor entre as placas para que ocorra a descarga. Se for um fio a descarga será instantânea, caso contrario o tempo de descarga dependerá da resistência.
No circuito da Figura 6a com a chave na posição A o capacitor se carregará instantaneamente até 12 V. Se a chave for colocada na posição B o capacitor se descarregara atraves da resistencia de 10 k e apos 4 constantes de tempo (40s) poderá ser consoderado descarregado.
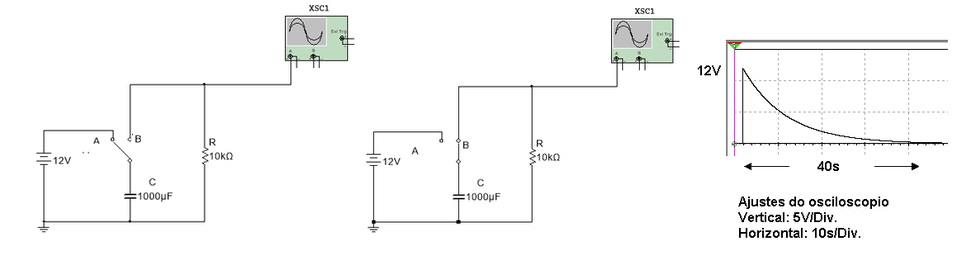
( a ) ( b ) ( c )
Figura 6 - Descarga do capacitor ( a ) Instante antes de fechar a chave ( b ) instante apos fechar a chave
Arquivo Multisim Live
Arquivo Multisim Live
A equação da tensão no capacitor em função do tempo é
Vc(t)=VCC.e-t/R.C
No caso do circuito, Vcc=12 V é a carga inicial R.C= 10 k.100k=10s, então apos 4 constantes de tempo o capacitor pode ser considerado descarregado na pratica.
Equação da tensão no capacitor em função do tempo: Vc(t)=12.e-t/10
Para t=0 Vc(0)=12 V para t=10 s Vc(10s)=0,37.12V = 4,44 V para t=40s Vc(40)=0,24 V
Se a resistencia e/ou a capacitancia forem alteradas o tempo de descarga muda. Por exemplo, se na Figura 6 o valor de R mudar para 1k a descarga será mais rapida. A Figura 7a mostra o circuito da Figura 6a com outro valor de resistencia, 1k. A constante de tempo agora é 1s. A Figura 7b mostra o grafico da descarga com os mesmos ajustes do osciloscopio.
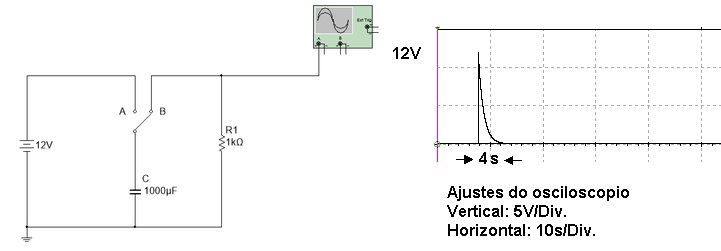
( a ) ( b )
Figura 7 - Diminuindo a constante de tempo ( a ) circuito (b ) Curva de de descarga do capacitor do circuito da Figura 6 para R=1K
A compreensão da carga e descarga são importante em muitas aplicações na eletronica, em circuitos de fonte de alimentação, geradores de forma de onda e circuitos integrador e diferenciador.
1.4 Associação de Capacitores
Capacitores são associados para a obtenção de valores maiores ou menores.
Paralelo
Quando capacitores são associados em paralelo, a capacitância aumenta, Figura 8. É o caso mais comum.
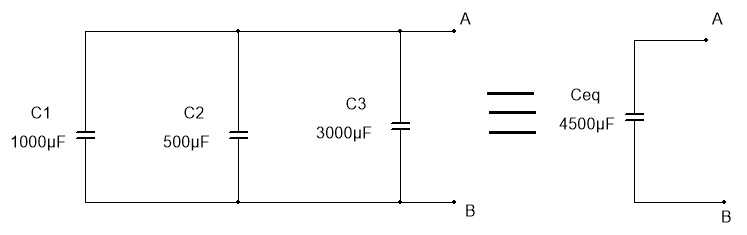
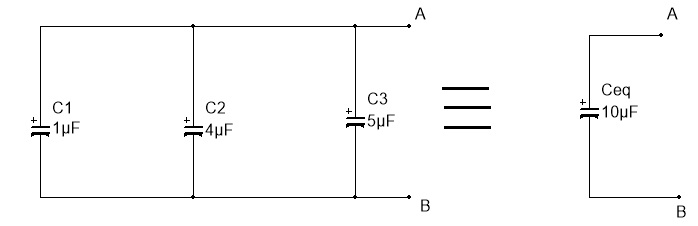
Figura 8 - associação paralelo de capacitores
O valor da capacitancia equivalente é dada por: CE=C1 + C2 +C3
Lembrando que se os capacitores tiverem polaridade, os positivos devem ser interligados entre si.
Serie
Quando capacitores são associados em serie, a capacitância diminui, Figura 9.
Quando capacitores são associados em serie, a capacitância diminui, Figura 9.
Figura 9 - Associação serie de capacitores
O valor da capacitancia equivalente é dada por:
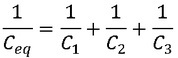
Que é a mesma espressão usada para obter o equivalente de resistencias em paralelo, portanto para o caso de dois capacitores o equivalente pode ser calculado por:
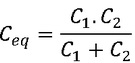
Exercícios Resolvidos
1) Dois capacitores C1=0,1mF e C2=0,4mF são ligados em paralelo. Calcule o valor do capacitor equivalente.
Solução: Como é uma associação paralelo então CE = C1 + C2 = 0,1 + 0,4 =0,5mF
2) Para um circuito RC serie é dada a curva de Vcxt. Sabendo-se que a fonte vale 10 V e que R=2 k qual o valor de C ?
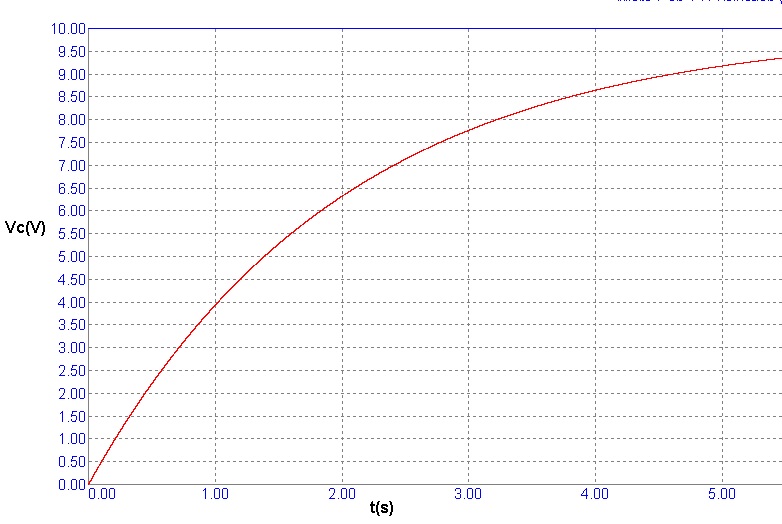
Solução:
Como a constante de tempo pode ser determinada a partir da curva (é o tempo necessário para que a tensão no capacitor atinja 6,3V) então tendo R poderemos determinar C.
Do gráfico obtemos que t= R.C = 2 s (aproximadamente) então C=2s/2k = 1000mF
Do gráfico obtemos que t= R.C = 2 s (aproximadamente) então C=2s/2k = 1000mF
2 Experiência: Carga e descarga do capacitor
2.1 Abra o arquivo ExpCA11_Carga_Descarga_do_Capacitor e identifique o circuito da Figura 10. Com a chave na posição A inicie a simulação.
Arquivo Multisim
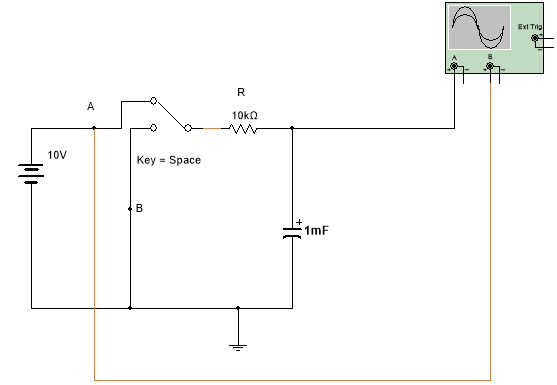
Figura 10 - Carga e descarga do capacitor
2.2 Usando o cursor, determine o tempo necessário para que o capacitor se carregue até 0,63.Vcc (no caso 6,3V). Anote esse tempo que é a constante de tempo, compare com o valor teórico. Obs: Pare a simulação, desligando a simulação, quamdo a tensão for aproximadamente 10V).
t(medido)_____________ t(calculado)_____________
2.3 Usando um curso verifique quanto tempo leva para que a tensão no capacitor atinja 98% da tensão da fonte (capacitor praticamente carregado). Verifique se está de acordo com a equação da carga do capacitor.
Tempo para 98% de Vcc=___________
2.4 Apos o capacitor estar totalmente carregado mude a posição da chave para a posição B, faça isso com o circuito ainda em simulação.
Obs: Para mudar a posição da chave a janela deve estar ativa. Para ativar a janela clique na parte superior onde se encontra o nome do arquivo.
Obs: Para mudar a posição da chave a janela deve estar ativa. Para ativar a janela clique na parte superior onde se encontra o nome do arquivo.
2.5 Escreva as suas conclusões.