aulaCA010 - eletronica24h
Menu principal:
aulaCA010
Educacional > Cursos > Eletricidade em CA
Analise de Circuitos em Corrente Alternada
Aula 10: Filtro Passa Baixas com Capacitor
Bibliografia
Analise de Circuitos em Corrente Alternada - Saraiva/Erica
1 Introdução
O circuito é semelhante ao FPA visto na aula anterior, com o R e o C trocando de posição, e por isso mesmo as suas características são opostas. O circuito é o da Figura 1a, a curva de resposta em freqüência do ganho esta mostrada na Figura 1b. A Figura 1c mostra a curva de resposta em frequencia da fase do ganho.
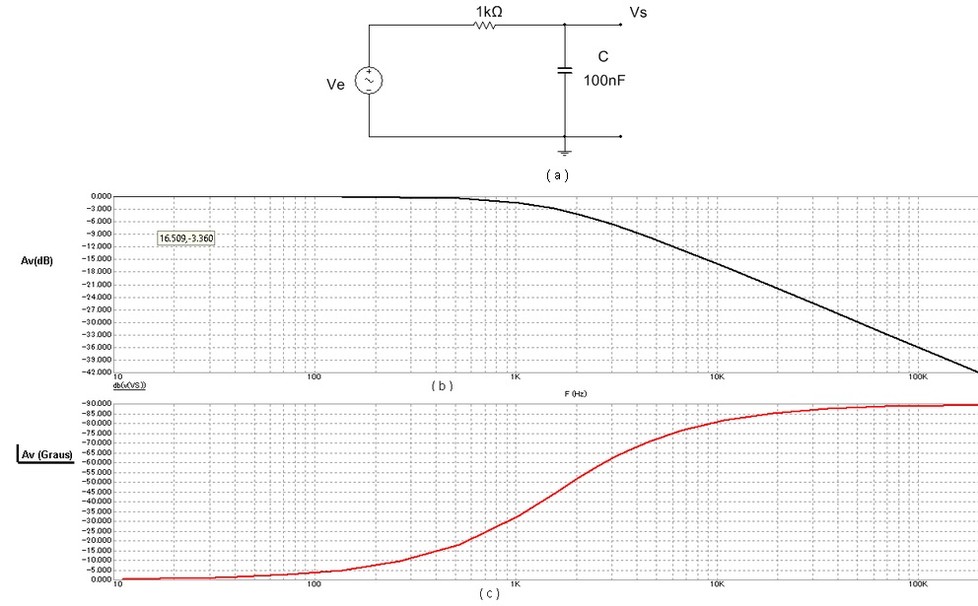
Figura 1 - (a ) Filtro Passa Baixas ( b ) curva de resposta em frequencia do modulo do ganho ( c ) curva de resposta em frequencia da fase do ganho
1.1 Modulo do Ganho e Fase do Ganho
O ganho é um numero complexo que tem modulo e fase. O modulo do ganho, que é função da frequencia, é dado por:
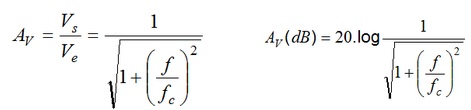
Observe que as expressões são semelhantes às do FPA. No FPB dentro do parentese é f/fc no FPA é fc/f. Atenção portanto!!!
A frequencia de corte, fc, é calculada da mesma forma:
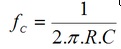
A relação entre a fase de Vs e a fase de Ve varia com a frequencia sendo dada pela curva de resposta em frequencia da fase do ganho
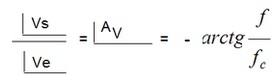
Se f=0 defasagem entre entrada e saida é nula e se f tender para infinito a defasagem tende pra -90 graus
Considere que o circuito da Figura 1a tem Ve=10 V, e que a fase de Ve é zero e f=fc, logo a defasagem do ganho é igual a -arctg1= -45 graus. Qual a fase do sinal de saida?
A defasagem entre a entrada e a saida na frequencia de corte é - 45 graus.
A Figura 2 mostra as formas de onda de entrada (preto) e saida (vermelho). Observar a defasagem de -45 graus entre a entrada e a saida. A Figura 2b mostra o Diagrama Fasorial dos dois sinais mostrando claramente que Vs está atrasado em relação a entrada de 45 graus. Este circuito muitas vezes é chamado de rede atraso. A amplitude da tensão de saida na frquencia de corte é de 7 V, pois o ganho nessa frequencia é 0,7.
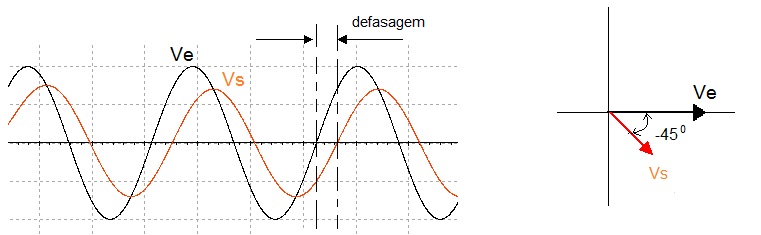
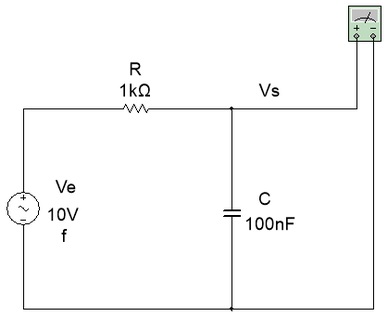
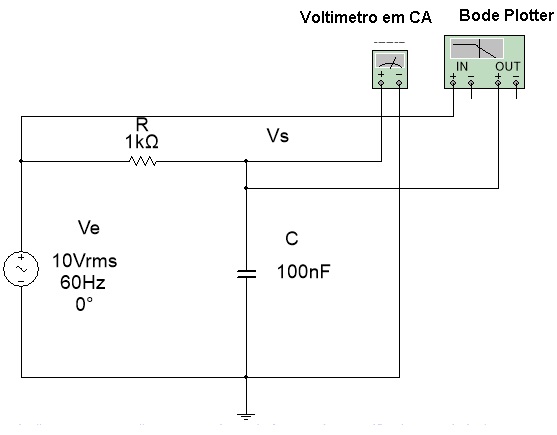

( a ) ( b )
Figura 2 - ( a ) Defasagem entre saida, Vs, e entrada, Ve, em um FPB ( b ) Diagrama Fasorial para os dois sinais, Ve e vs, na frequencia de corte
Fonte: Multisim V. 14
Figura 2 - ( a ) Defasagem entre saida, Vs, e entrada, Ve, em um FPB ( b ) Diagrama Fasorial para os dois sinais, Ve e vs, na frequencia de corte
Fonte: Multisim V. 14
2 Exercicio resolvido 1
Para o circuito determinar:
a) frequencia de corte
b) Valor da saida (Vs) na frequencia de 3 kHz se Ve=10 V
c) Observe as formas de onda de entrada (ve) e saida (Vs) para f<<<<<<fc (ao menos 100 vezes menor)
d) Observe as formas de onda de entrada (Ve) e saida (vs) para f=fc
e) Observe as formas de onda de entrada (Ve) e saida (Vs) para f>>>>>fc (ao menos 100 vezes maior)
d) Valor da saida se Av= -15 dB. Qual a frequencia? Se não conseguir algebricamente usando a equação do ganho, use a curva de resposta em frequencia.

Figura 3 - FPB para exercicio 1
Solução:
b) Para determinar o valor da tensão na saida, Vs, primeiramente o valor do ganho em 3 kHz deve ser determinado usando a expressão do ganho (Av=Vs/Ve)
Logo a tensão de saida será: Vs=Av.Ve = 0,47.10V=4,7 V
c) Novamente deve ser determinada a relação entre a saida e a entrada, Vs/Ve. Como foi dado o ganho em dB. Voce deve usar a sua calculadora cientifica para essa operação.
Se Av= -15dB=20.log(Vs/Ve) então log (Vs/Ve)= -0,75 na maquina use a função inversa de logx voce obterá Vs/Ve=0,178.
E exatamente como no exercicio do FPA, use a expressão do modulo do ganho. Entre com Vs/Ve=0,178.
Dica: Eleve ao quadrado dos dois lados da igualdade para desaparecer a raiz quadrada.
Resolvendo obtem-se f=12 kHz
Para verificar, faça o caminho contrario. Entre com essa frequencia na expressão do ganho, voce deve obter 0,178.
3. Experiencia: Filtro Passa Baixas (FPB)
3.1. Abra o arquivo ExpCA016 Filtro Passa Baixas (Multisim 14) e identifique o circuito da Figura 4. Inicie a simulação, e para cada frequencia da tabela 1, meça o valor da saida (Vs) anotando na tabela 1.
Arquivo Multisim Live
Arquivo Multisim Live

Figura 4 - Filtro Passa Baixas para experiencia
Tabela 1 - FPB - curva de resposta em frequencia
| f(Hz) | 500 | 800 | 1 k | 2 k | 4 k | 8 k | 10 k | 15 k | 20 k | 30 k |
Vs/Ve | ||||||||||
20.logVs/Ve |
3.2. Com os dados da tabela 1 desenhe o grafico do ganho em dB em função da frequencia e para isso use papel monolog.
3.3. A partir do grafico obtenha a frequencia de corte (frequencia na qual o ganho vale -3dB).
3.4. Insira um osciloscopio com o canal A ligado na entrada, Ve, e o canal B na saida, Vs. Ajuste a frequencia de Ve em fc. Inicie a simulação e meça a defasagem entre Vs e Ve. Para isso meça primeiramente a defasagem no tempo e para isso use os dois cursores. Transforme para graus e anote os valores medidos e teoricos.
Defasagem(f=fc)=___________(valor teorico) Defasagem(f=fc)=___________(valor medido)
3.5. Escreva as suas conclusões.
4. Filtro como separador de sinais
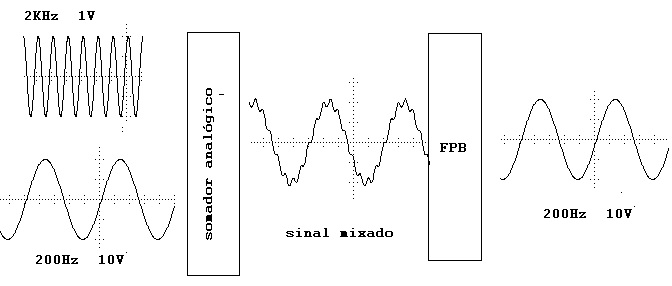
É a aplicação que de fato justifica o nome de filtro e que consiste em separar sinais de freqüências diferentes. Na Figura 5 dois sinais são somados, um de f1=2 kHz, 1 Vpico e outro de f2=200 Hz e 10 Vpico. O sinal mixado (somado) é obtido. Se o sinal somado é aplicado a um FPB de frequencia de corte 250 Hz, na saida o sinal de 200 Hz é obtido novamente.
Arquivo Multisim Live

Figura 5 - Filtro Passa Baixas separando duas frequencias
5. Experiencia: FPB como Separador de Frequencias
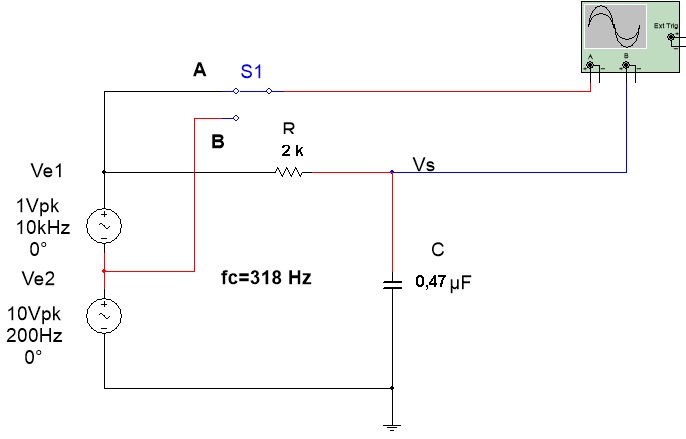
5.1. Abra o arquivo ExpCA17_Circuito separador de frequencias (Multisim 14) e identifique o circuito da Figura 6. Inicie a simulação e observe as formas de onda em A (soma de Ve1 +Ve2) em B (somente sinal que deve passar, Ve2) e na saida Vs.
5.2. Experimente mudar a frequencia e amplitude do ruido, Ve1, para ver a influencia na separação. Aumente a amplitude para 4 V e diminua a frequencia para 2 kHz.

Figura 6 - Circuito separador de freqeuncias
Arquivo Multisim Live
5.3. Escreva as suas conclusões
