aulaCA009 - eletronica24h
Menu principal:
aulaCA009
Educacional > Cursos > Eletricidade em CA
Analise de Circuitos em Corrente Alternada
Aula 09: Filtros
Bibliografia
Analise de Circuitos em Corrente Alternada - Saraiva/Erica
1 Introdução
O decibel (dB) é uma unidade logarítmica usada para relacionar duas grandezas (potencia elétrica, potencia sonora, tensão, corrente, etc). Em eletrônica as grandezas relacionadas constumam ser tensão, corrente e potencia. A Figura 1 mostra um quadripolo (dispositivo ou sistema com 4 terminais) generico para o qual a variavel de entrada é tensão, Ve, e a variavel de saida é tensão, Vs. A relação entre a tensão de saida e a tensão deentrada determina o ganho de tensão.
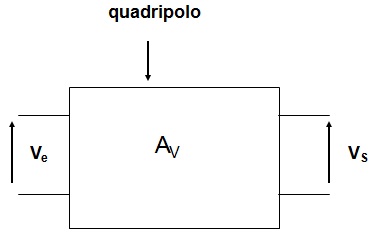
Figura 1 - Quadripolo
1.1 Ganho de tensão do quadripolo
Define-se o ganho de tensão de um quadripolo como sendo a relação entre a tensão de saida, Vs, e a tensão de entrada, Ve. Como são grandezas complexas, o ganho Av tambem será uma grnadeza complexa (modulo e fase).

Ex: Ve=1 V e Vs= 10 V logo o ganho de tensão vale: Av=Vs/Ve = 10 V/1 V = 10, Av=10 significa que a saida é 10 vezes maior do que a entrada, então se para o mesmo circuito Ve=0,2 V então a saida será igual a Vs=10.0,2 V = 2 V (existem limites para essa relação ser verdade, mas isso não será estudado nessa aula), e o ganho tambem depende da frequencia de Ve.
O ganho tambem pode ser especificado de outra forma, em decibeis (dB) existindo uma razão para isso. Em dB o ganho é dado por:
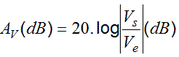
Então, se Ve=1V e Vs=10 V o ganho em dB valerá:
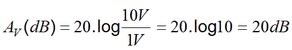
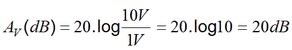
Exercicio Resolvido 1: Determinar o ganho (Vs/Ve) e em dB do circuito.
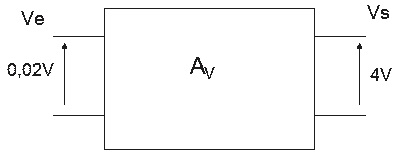
Figura 2 - Quadripolo com Ve=0,02 V e Vs=4 V
Para o quadripolo da Figura 2 o ganho de tensão vale:

ou em decibeis (dB):
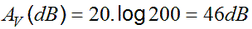
Então observe que Av(dB) > 0 haverá amplificação
Considere o quadripolo da Figura 3, onde Ve=10 V e Vs=0,2 V
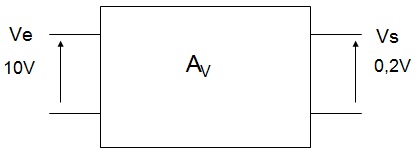
Figura 3 - Quadripolo com Ve=10 V e Vs=0,2 V
O ganho de tensão vale:
Av=0,2V/10V=0,02
O ganho de tensão em dB vale:
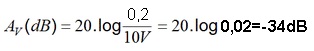
Observe que, se Av(dB) < 0 haverá atenuação
Se Ve=Vs, Figura 4, nesse caso o ganho de tensão vale AV=Vs/Ve=1 (saida igual a entrada) e o ganho em dB será AV(dB)20.log(Vs/Ve)=0 dB
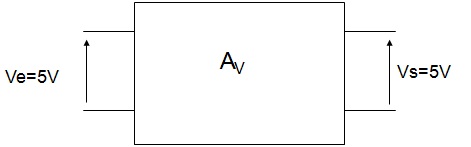
Figura 4 - Quadripolo com ganho igual a 1
2 Filtros Passivos
São filtros construidos com resistores, capacitores e indutores. Para esses filtros a saida nunca será maior que a entrada, portanto o ganho será sempre menor ou igual a 1 ou em dB < odB Para obter uma saida maior que a entrada devem ser usados filtros ativos que alem disso tem uma seletividade muito grande. São construidos com amplificadores operacionais, estudados em outro curso.
Os filtros podem ser classificados em
2.1 Filtro Passa Altas (FPA)
A Figura 5a mostra o quadripolo que é um FPA (Filtro Passa Altas), e a Figura 5b mostra o grafico do Ganho em função da frequencia (Avxf), tambem chamado de Curva de Resposta em Frequencia. O filtro ideal é representado pelo grafico em preto, enquanto o filtro real em vermelho. . No grafico existe uma frequencia caracteristica do circuito chamada de frequencia de corte, fc. Na frequencia de corte o ganho de tensão tem uma valor particular, Av=0,707.
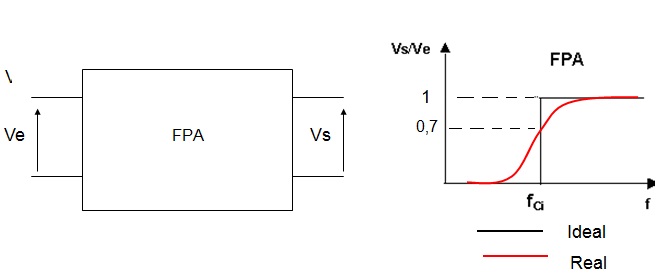
( a ) ( b )
Figura 5 - ( a ) quadripolo que representa um FPA ( b ) curvas de resposta e frequencia do FPA, ideal e real
O que significa o grafico ideal da Figura 5b? Que se f < fci Vs=0, para f>=fci Vs=Ve (caso Ideal). Na pratica existe uma saida se f<fc. Quanto menor for f em relação a fc, menor será a saida.
2.2 Filtro Passa Baixas (FPB)
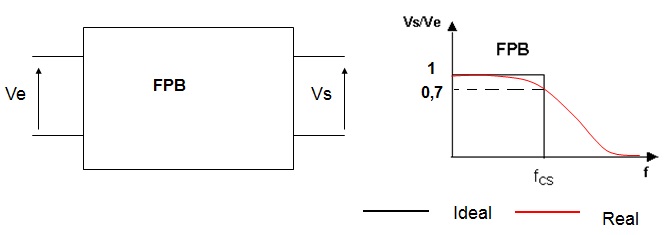
A Figura 6a mostra o quadripolo que é um FPB, e a Figura 6b mostra o grafico do ganho em função da frequencia (Avxf) para um filtro ideal (em preto) e filtro real (em vermelho). No grafico existe uma frequencia caracteristica do circuito chamada de frequencia de corte, fc. Na frequencia de corte o ganho de tensão tem uma valor particular, Av=0,707.
( a ) ( b )
Figura 6 - ( a ) quadripolo que representa um FPB ( b ) curvas de resposta e frequencia do FPB, ideal e real
O que significa o grafico ideal da Figura 5b? Que se f > fci Vs=0, para f<=fci Vs=Ve (caso Ideal). Na pratica existe uma saida se f>fc. Quanto maior for f em relação a fc, menor será a saida.
2.3 Filtro Passa Faixa (FPF) e Filtro Rejeita Faixa (FRF)
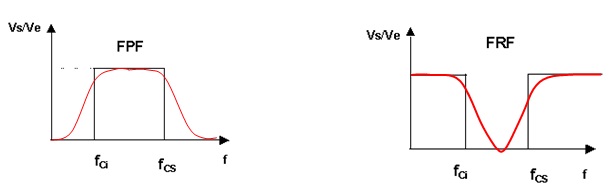
Esses filtros não serão estudados nesse curso, as suas curvas estão mostradas na Figura 7a, FPF e Figura b, FRF.
( a ) ( b )
Figura 7 - ( a ) Filtro Passa Faixa ( b ) Filtro Rejeita Faixa
3 Filtro Passa Altas
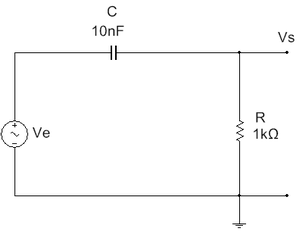
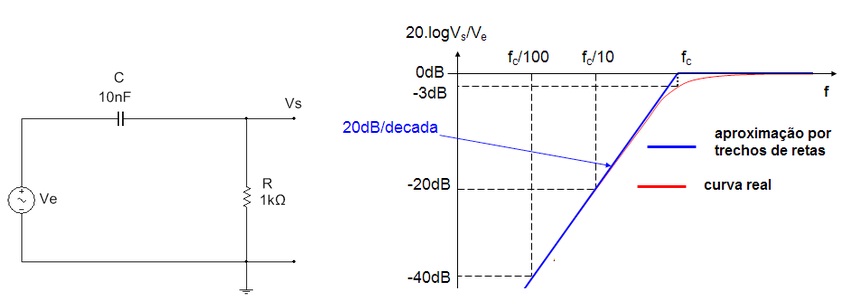
O FPA pode ser obtido com um circuito RL ou circuito RC serie (caso mais comum). Para saber como construir com RL serie consultar o livro Analise de Circuitos em CA. A Figura 8 mostra um circuito RC serie onde a tensão de saida é obtida no resistor, Vs=VR. A relação entre Vs e VR, Vs/VR determina o ganho que é um numero complexo com modulo e fase.
( a ) ( b )
Figura 8 - ( a ) Filtro Passa Altas (FPA) ( b ) curva de resposta em frequencias
Figura 8 - ( a ) Filtro Passa Altas (FPA) ( b ) curva de resposta em frequencias
Qual o significado do gráfico da Figura 8b? Para frequencias muito acima da frequencia de corte, fc, o ganho é 1 (0dB), isto é, a saida será igual à entrada (ganho=1 ou 0dB).
Para freqüências muito abaixo da de corte o ganho diminui. Por exemplo, se f=fc/10 o ganho é 0,1 ou -20 dB. toda vez que a freqüência diminui de 10 vezes (variação de uma década), o ganho varia de 10 vezes. Por exemplo se a frequencia varia de fc/10 para fc/100 (1 decada de variação), o ganho diminui de 10 vezes, passa de -20dB para -40db. Dizemos que a inclinação da curva na parte reta é de -20dB/decada ou -6dB/oitava. Essa inclinação é sempre -20dB/decada para filtros passivos. Para filtros ativos pode-se obter de 80dB/decada, 100dB/decada, etc o que significa uma grande seletividade.
3.1 Modulo do ganho e fase do ganho
No circuito da Figura 8a a tensão de saida, Vs, é obtida na resistencia R sendo dada por (expressão do divisor de tensão):
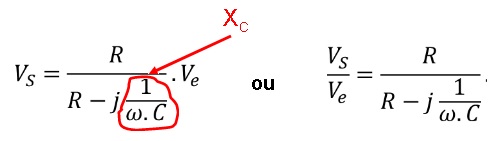
Portanto o ganho (Vs/Ve) é um numero complexo cujo modulo é dado por:
O Ganho em função da frequencia é dado por:
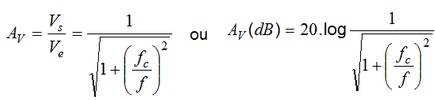
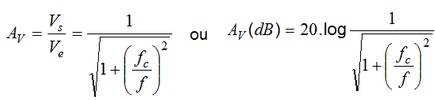
Onde fc é a frequencia de corte calculada por:
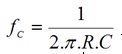
Para cada valor de frequencia o ganho (Vs/Ve) ou 20.log(Vs/Ve) tem um valor, assim é que se f=fc substituindo na equação do ganho em função da frequencia resulta:
Av=Vs/Ve=0,707 e 20.log0,707=-3dB
A relação entre a fase de Vs e a fase de Ve varia com a frequencia sendo dada por:
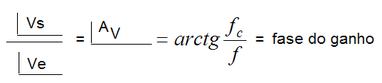
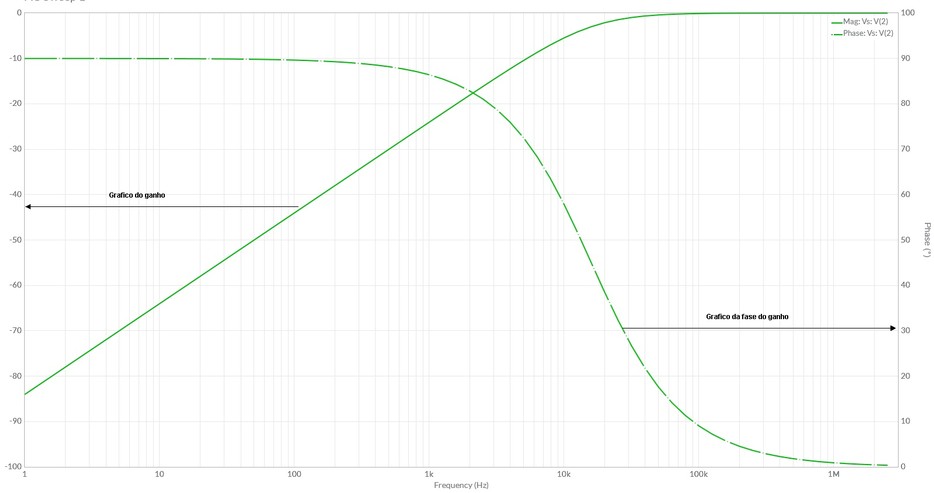
Significa que na frequencia de corte, a fase do ganho é 45 Graus, isto é, se a fase do sinal de entrada é 0 Graus a fase da saida será -45 Graus. A Figura 9 mostra o grafico da fase do ganho do circuito da Figura 8 e do modulo do ganho, em dB.
Curva de Resposta em Frequencia do Ganho e da fase do ganho
Na Figura 9 observe que a medida que a frequencia de aproxima de zero (CC) a fase do ganho tende para 90 graus, isto é, o circuito se comporta como se fosse praticamente capacitivo (Xc>>>>R). Ao contrario, se a frequencia aumentar muito Xc<<R, tudo se passa como se o capacitor se comporte como um curto circuito, e toda a tensão de entrada aparece na saida (Vs=Ve e ganho =1) e a diferença de fase entre Vs e Ve é zero.
3.2 Exercicio resolvido 1
Para o circuito determinar:
a) frequencia de corte (Cheque a resposta usando o arquivo Multisim Live)
b) valor da saida (Vs) na frequencia de 5 kHz se Ve=10 V (Cheque a resposta usando o arquivo Multisim Live)
c) Para que frequencia a saida é 0,5 V. (Cheque a resposta usando o arquivo Multisim Live)
b) valor da saida (Vs) na frequencia de 5 kHz se Ve=10 V (Cheque a resposta usando o arquivo Multisim Live)
c) Para que frequencia a saida é 0,5 V. (Cheque a resposta usando o arquivo Multisim Live)
Solução:
b) Usando a expressão do ganho, o ganho em 5 kHz é calculado por:
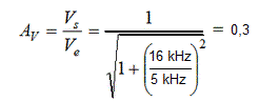
Logo o valor da saida em 5 kHz será igual a: Vs=Av.Ve= 0,3.10V=3 V
Um caminho alternativo é calcular a impedancia Z.
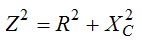
Onde
Xc=1/(2.p.f.C)=1/(2.p.5kHz.10nF)=3.183 W
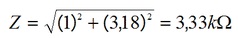
Logo o valor da corrente será:
I=10V/3,33k =3 mA e o valor da tensão em R que é a tensão de saida será igual a Vs=1k.3mA = 3 V e o valor do ganho AV=Vs/Ve = 3 V/10 V= 0,3.
I=10V/3,33k =3 mA e o valor da tensão em R que é a tensão de saida será igual a Vs=1k.3mA = 3 V e o valor do ganho AV=Vs/Ve = 3 V/10 V= 0,3.
c) Vs=0,5 V significa um ganho de Av=0,5V/10V =0,05 voce deve entrar com esse valor na expressão AVxf e determinar f.
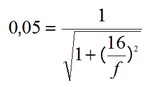
Dica: Eleve ao quadrado dos dois lados da igualdade eliminando a raiz
O resultado é f=0,8 kHz=800 Hz
Obs: Faça o caminho contrario, isto é, entre com 0,8 kHz na expressão do ganho para determinar o ganho. Voce deve determinar 0,05.
Poderia tambem determinar graficamente. Primeiro determinando o ganho em dB. Se voce tiver o grafico (pode obter no Multisim 14 usando o instrumento chamado Bode Plotter ou no Multisim Live analise ACSweep). Entre com o ganho, Av(dB)=20.log0,05 = -26dB, e leia a frequencia, Figura 10. O problema é que a escala de frequencia é LOGARITMICA, se a frequencia não for um multiplo inteiro de 10 é dificil obter precisão.
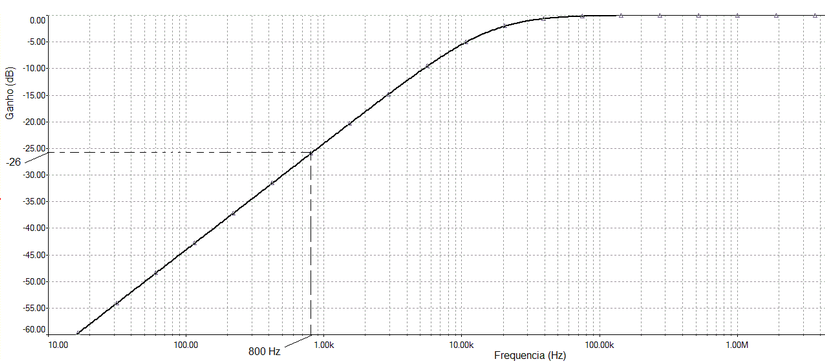
Figura 10 - Curva de resposta em frequencia do circuito da Figura 8 - Determinando aem que frequencia o ganho é -26dB.
4 Experiencia: Filtro Passa Altas
4.1 Abra o arquivo ExpCA14_Filtro_Passa_Altas (Multisim 14) e identifique o circuito da Figura 11. Inicie a simulação, e para cada frequencia da tabela 1, meça o valor da saida (Vs) anotando na tabela 1. Observe que a entrada é 10V, e a medida é feita com um voltimetro na saida(Vs).
Obs: Usando Multisim 14
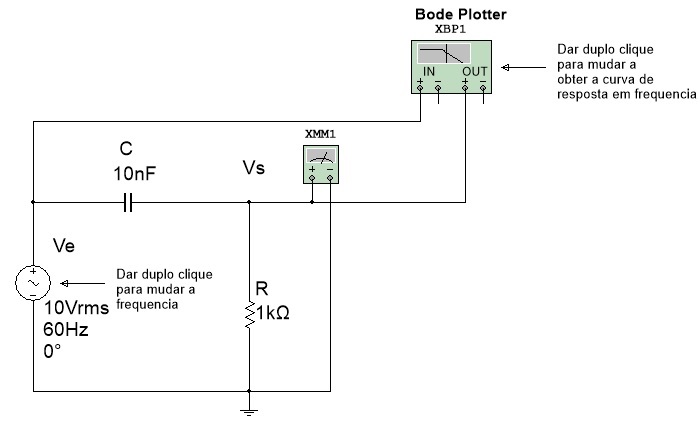
Figura 11 - FIltro Passa Altas para experiencia
Tabela 1 - FPA - curva de resposta em frequencia
| f(Hz) | 100 | 500 | 1k | 5k | 10k | 13k | 15k | 18k | 20k | 30k |
Vs/Ve | ||||||||||
| 20.logVs/Ve |
4.2 Com os dados da tabela 1 desenhe o grafico do ganho em dB em função da frequencia e para isso use papel monolog.
4.3 A partir do grafico obtenha a frequencia de corte (frequencia na qual o ganho vale -3dB).
4.4 escreva as suas conclusões.
5 Experiencia: O Decibel
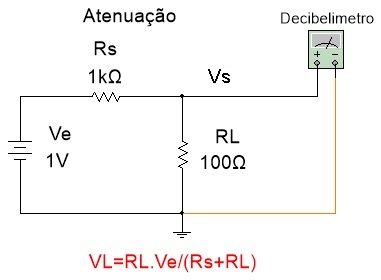
5.1 Abra o arquivo ExpCA15_O_decibel (Multisim 14)e identifique o circuito da Figura 12. Calcule o ganho (Vs/Ve) e o ganho em dB (20.logVs/Ve) e anote na tabela 2. Nesse caso existe atenuação.
5.2 Inicie a simulação. Para cada caso abra o Decibelimetro e em Set... (Settings) ajuste dB relative value para 1 V Ve).
Obs: O Decibelimetro so existe no Multisim 14 Atenção!!!!!!
Obs: O Decibelimetro so existe no Multisim 14 Atenção!!!!!!

Figura 12 - Medindo o ganho em dB quando há atenuação
Tabela 2 - Ganho calculado e medido
| Calculado | Medido | ||
| VL/Ve | 20.log(VL/Ve) | VL/Ve | 20.log(VL/Ve) |
5.3 Abra o arquivo ExpCA15_O_decibel (Multisim 14) e identifique o circuito da Figura 13. Calcule o ganho (VL/Ve) e o ganho em dB (20.logVL/Ve) e anote na tabela 3
5.4. Inicie a simulação. Para cada caso abra o Decibelimetro e em Set... (Settings) ajuste dB relative value para 1 V Ve).Obs: O circuito é um amplificador com um C.I chamado Amplificador Operacional.
O ganho de tensão Av=Vs/Ve para os valores de resistencias do circuito é 10.
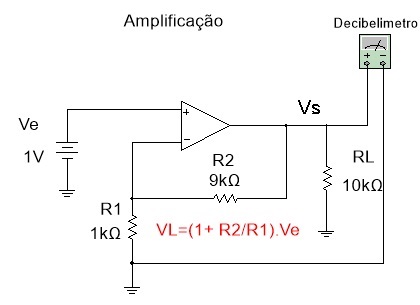
Figura 13 - Medindo o ganho em dB quando há amplificação
Tabela 3 - Ganho calculado e medido
| Calculado | Medido | ||
| VL/Ve | 20.log(VL/Ve) | VL/Ve | 20.log(VL/Ve) |
5.5. Abra o arquivo ExpCA15_O_decibel (Multisim 14) e identifique o circuito da Figura 14. Calcule o ganho (VL/Ve) e o ganho em dB (20.logVL/Ve) e anote na tabela 4
5.6 Inicie a simulação. Para cada caso abra o Decibelimetro e em Set... (Settings) ajuste dB relative value para 1 V Ve).
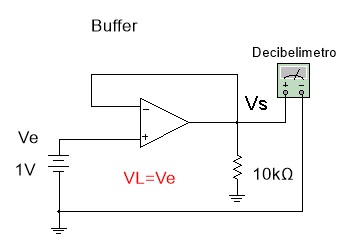
Figura 14 - Medindo o ganho em dB quando a saida é igual a entrada (Buffer)
Tabela 4 - Ganho calculado e medido
| Calculado | Medido | ||
| VL/Ve | 20.log(VL/Ve) | VL/Ve | 20.log(VL/Ve) |
5.7 Escreva as suas conclusões