aulaCC010 - eletronica24h
Menu principal:
aulaCC010
Educacional > Cursos > Eletricidade em CC
Analise de Circuitos em Corrente Contínua
Aula 10: Divisor de Tensão
Referencias
Analise de Circuitos em Corrente Continua - Rômulo O. Albuquerque - Editora Érica
Aula 10: Divisor de Tensão
Referencias
Analise de Circuitos em Corrente Continua - Rômulo O. Albuquerque - Editora Érica
1 Divisor de tensão sem carga
Como já visto em aulas anteriores, um divisor de tensão é um circuito serie, figura 1. Se a tensão de entrada é a tensão da bateria, E, e a tensão de saída é obtida em uma das resistências, R2, o seu valor será dado por:
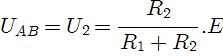
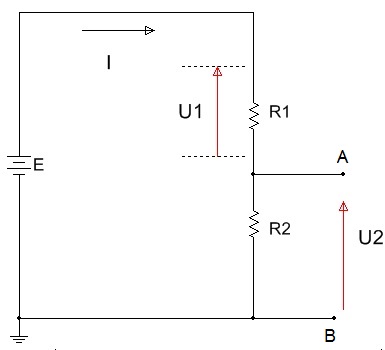
Figura 1 - Divisor de tensão sem carga
Caso seja conectado uma uma resistência entre A e B, de valor RL, o valor da tensão entre A e B diminuirá pelo efeito de carga exercido por essa resistência, pois o valor efetivo da resistência entre A e B agora será R2//RL, Figura 2.
2 Divisor de tensão com carga
Se adicionarmos uma resistência ao divisor de tensão da Figura 1, o efeito de carga exercido por essa resistência diminuirá a tensão (em relação ao valor sem carga). A expressão da tensão na carga (RL) será:
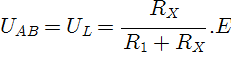
onde Rx=R2//RL
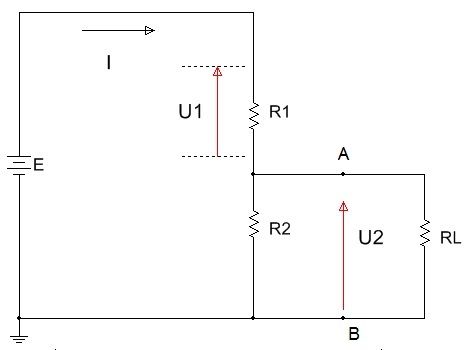
Figura 2 - Divisor de tensão com carga
Como Rx < R2 então a tensão entre A e B, UAB, com carga, será menor do que UAB sem carga. A isso chamamos "Efeito de Carga
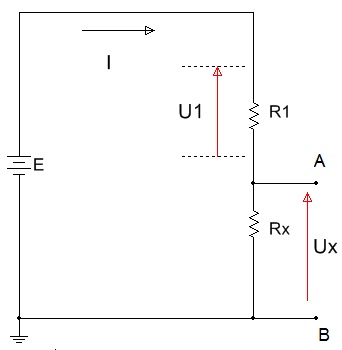
Figura 3 - Divisor de tensão com carga - circuito equivalente
3 Exercicios resolvidos
3.1 Seja o divisor de tensão da Figura 4.Seja RL a resistência conectada em paralelo com R2. Calcule a tensão indicada pelo voltímetro para 3 casos:
a) RL infinito
b) RL = 15 k, chave A para baixo e chave B para baixo
c) RL=150 k, portanto RL>>> R2 =15 k, chave A para baixo e chave B para cima.
a) RL infinito
b) RL = 15 k, chave A para baixo e chave B para baixo
c) RL=150 k, portanto RL>>> R2 =15 k, chave A para baixo e chave B para cima.
Solução:
a) RL infinito (sem carga), chave A para cima.
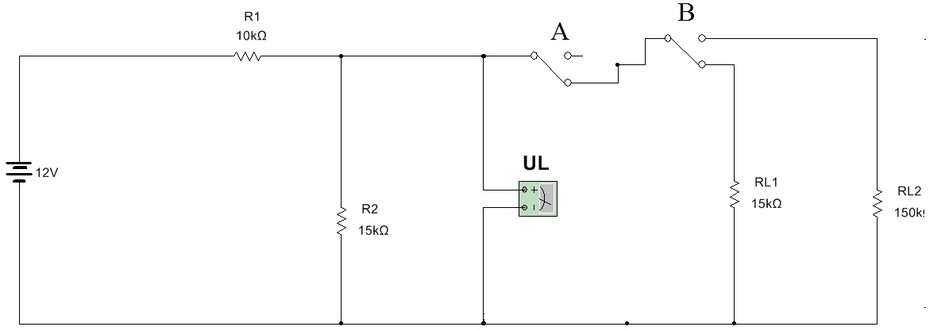
Figura 4 - Divisor de tensão em três situações - sem carga - carga baixa - carga alta
Caso a - carga infinita ( Chave A para cima):
Nesse caso: | 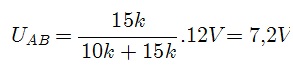 |
Caso b - RL =15 k
(chave A para baixo chave B para baixo)
Nesse caso o efeito de carga de RL será Rx=R2//RL = 15k//15k =7,5 k
Nesse caso o efeito de carga de RL será Rx=R2//RL = 15k//15k =7,5 k
E portanto a tensão UAB valerá: | 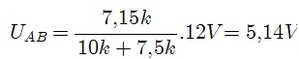 |
Caso c - RL =150 k ( chave A para baixo cahve B para cima)
Nesse caso o efeito de carga de RL será: Rx=15k//150k =13,6 k
E portanto a tensão UAB valerá: | 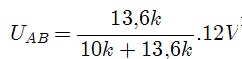 |
Como pode ser verificado, no ultimo caso o efeito de carga é pequeno (a tensão com carga e sem carga tem praticamente o mesmo valor), pois o valor da carga (RL) é muito alto quando comparado com a resistencia que tem em paralelo.
Atenção!!! RL deve ser muito maior que R2//R1, quando você estudar o teorema de Thevenin entenderá melhor essa questão.
Atenção!!! RL deve ser muito maior que R2//R1, quando você estudar o teorema de Thevenin entenderá melhor essa questão.
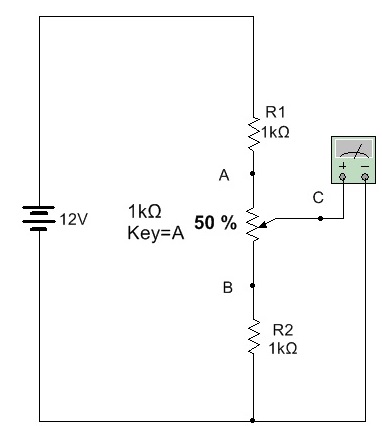
3.2 Para o divisor com potenciômetro calcule a máxima e a minima tensão indicada pelo voltimetro. apos resolver o exercicio use o Multisim Live para verificar. Clique no circuito para acessar o arquivo.
Solução:
O potenciometro tem duasposições limites: todo horario (no desenho o cursor todo para cima) e todo anti horario (no desenho o cursor todo para baixo).
Seja o cursor todo para cima resulta o circuito:
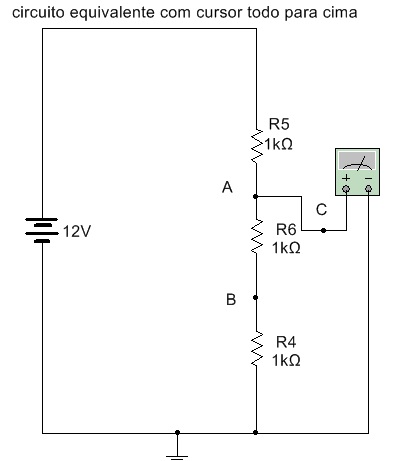
Pode ser usada a expresão do divisor de tensão, onde a resistencia em cima da qual se quer a tensão é R6+R7=2 k, portanto a tensão vale:
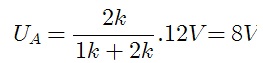
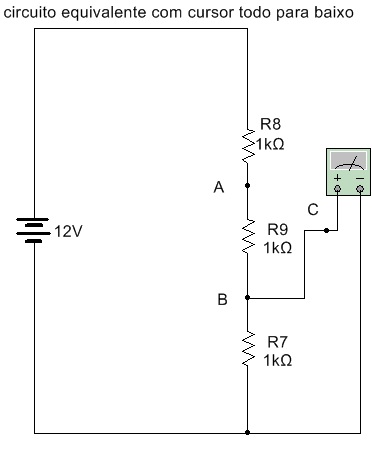
Seja o cursor todo para baixo, resulta o circuito:
Nesse caso a resistencia em cima da qual a tensão está sendo medida é 1 k, a outra resistencia é R8+R9=2 k, logo a tensão vale:
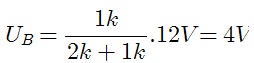
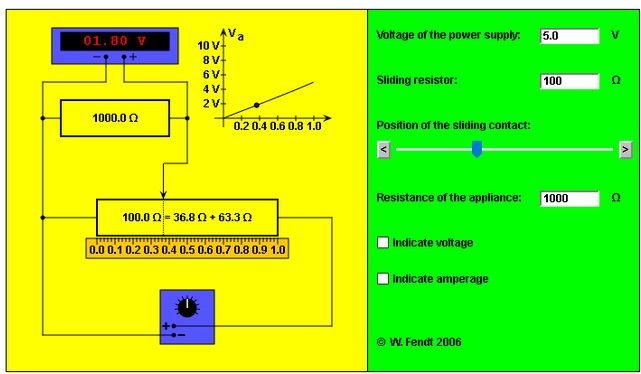
A seguir uma aplicação Java que mostra um divisor de tensão ajustavel onde a tensão é obtida no cursor. Ver o circuito ao lado para entender melhor o circuito.
4 Experiência: Divisor de Tensão com Carga
4.1 Abra o arquivo ExpCC08 Divisor de Tensão com Carga e identifique o circuito da Figura 5. Calcule a tensão entre A e B para todas as combinações das chaves 1 e chave 2, anotando os valores na tabela 1.
4.2 Inicie a simulação e meça a tensão entre A e B para todas as combinações das chaves 1 e chave 2 anotando os valores na tabela 2.
Link para Multisim Live
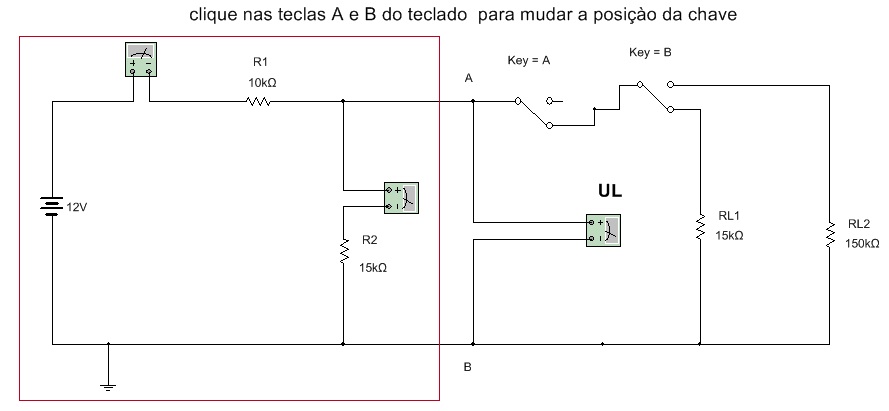
Figura 5 - Divisor de tensão com Carga
Tabela 1 - Divisor de tensão com carga, valores calculados
Valores Calculados | ||
Chave1 para baixo | Chave 1para cima e 2 para baixo | Chave 1 para cima e 2 para cima |
UAB | UAB | UAB |
Tabela 2 - Divisor de tensão com carga, valores simulados
Valores Simulados | ||
Chave1 para baixo | Chave 1para cima e 2 para baixo | Chave 1 para cima e 2 para cima |
UAB | UAB | UAB |
4.3 Compare os valores simulados com os valores calculados
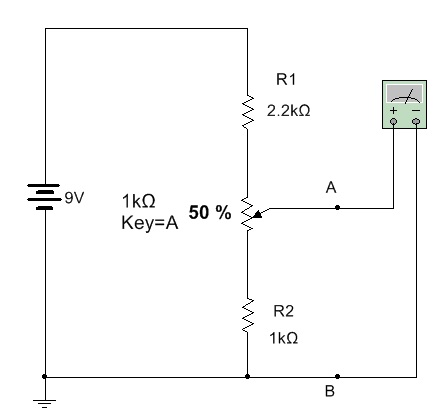
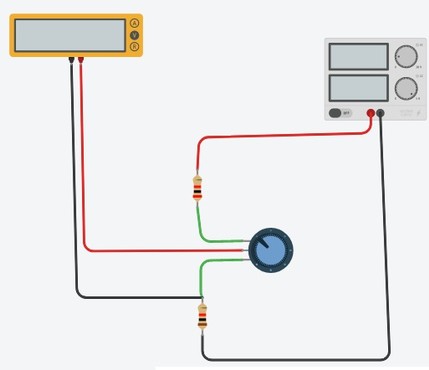
4.4 Abra o arquivo ExpCC09 Divisor de Tensão Ajustavel e identifique o circuito da figura 6. Calcule os valores máximo e mínimo para a tensão entre A e B. Anote os valores calculados na tabela 3.
Link para Multisim Live

( a ) ( b )
Figura 6 - Divisor de tensão ajustavel ( a ) Multisim 14 ( b ) Tinkercad
4.5 Inicie a simulação abrindo o arquivo ExpCC09 Divisor de Tensão Ajustavel meça a tensão para o Rv nos dois limites (100% e 0%) ou use a letra A maiuscula para variar em um sentido e a letra a minuscula para variar no sentido contrario. Anote os valores medidos na tabela 3.
Tabela 3 - Divisor ajustavel, valores calculados e medidos
Calculado | Medidos | ||
Umin | Umáx | Umin | Umáx |
4.6. Conclusões:
5 Exercícios Propostos
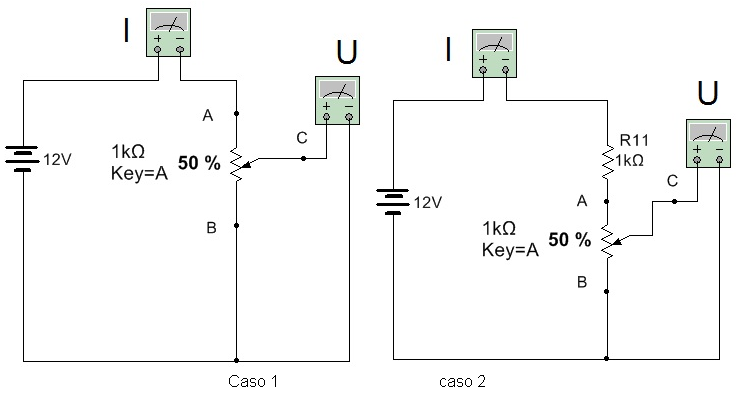
5.1 Para cada caso qual a indicação dos instrumentos para tres condições: a) Cursor todo para cima b) Cursor no meio c) Cursor todo para baixo.
Caso 1 caso 2
Resolva a Prova 2. Para se considerar aprovado voce deve acertar pelo menos 60% das questões.
Eletricidade Basica: Curva caracteristica - Potencia - Energia - Associação serie e paralelo de resistencias
Voce tem 60minutos para completar os testes. Tenha em mãos calculadora, caneta e rascunho
Qualquer dúvida consulte o capítulo 4.3 do livro Analise de Circuitos em Corrente Continua - Rômulo O. Albuquerque - Editora Érica