aulaDC04 - eletronica24h
Menu principal:
aulaDC04
Educacional > Cursos > Digital Combinacional
ELETRÔNICA DIGITAL - CIRCUITOS COMBINACIONAIS
Aula 04: Função OU Exclusivo - Função Coincidência - Equivalência entre Portas Lógicas
Prof Me. Romulo Oliveira Albuquerque
1. Equivalencia entre portas logicas
Dado um circuito logico o mesmo pode ser implementado de varias formas. Em geral o circuito otimizado é aquele que usa o menor numero de CIs, não esqueça que em um CI pode ter mais de uma porta logica. Por exemplo o CI 7400 tem 4 portas NAND de duas entradas.
1.1. Função OU Exclusivo - Porta OU Exclusivo (XOR)
Essa função e a porta lógica correspondente formam juntamente com a coincidência outros circuitos básicos de sistemas digitais.
A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Símbolo | Expressão Lógica |
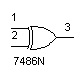 | 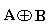 |
( a ) ( b ) ( c )
Figura 1 - Função OU EXCLUSIVO ( a ) Símbolo ( b ) Expressão Lógica ( c ) Tabela Verdade
2. Função COINCIDÊNCIA - Porta COINCIDÊNCIA (XNOR)
Figura 1 - Função OU EXCLUSIVO ( a ) Símbolo ( b ) Expressão Lógica ( c ) Tabela Verdade
A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Símbolo | Expressão Lógica |
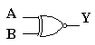 | 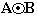 |
( a ) ( b ) ( c )
Figura 2 - Função Coincidencia ( a ) Simbolo ( b ) Expressão logica ( c ) tabela verdade
Figura 2 - Função Coincidencia ( a ) Simbolo ( b ) Expressão logica ( c ) tabela verdade
1.2. Equivalência entre blocos lógicos
Quando desejamos construir na prática um circuito lógico deveremos minimizar ao máximo possível os custos, por exemplo diminuindo ao máximo o número de CI's usados. Por outro lado muitas vezes não dispomos de uma determinada porta lógica e mas podemos usar outra porta fazendo a equivalência.
1.2.1. Obtendo um inversor a partir de NE
Para obter uma porta inversora usando porta NE, a Figura 3 mostra duas possibilidades.
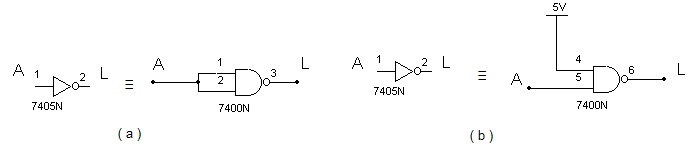
Figura 3 - Obtendo a função NÃO a partir de porta NE
1.2.2. Obtendo um Inversor a partir de NOU
Para obter uma porta inversora usando portas NOU temos as duas possibilidades:

Figura 4 - Obtendo a função NÃO a partir da função NOU
1.2.3. Obtendo NOU e OU partir de NE, E e inversores
Essas equivalências são obtidas considerando o Teorema de De Morgan.
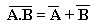
e
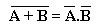
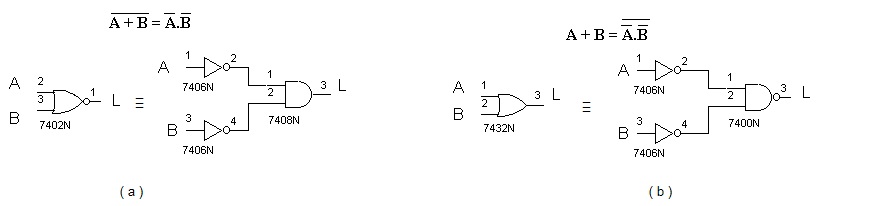
Figura 5 - Obtendo a função NOU e OU a partir da função NE e E
1.2.4. Obtendo NE e E partir de OU, NOU e inversores
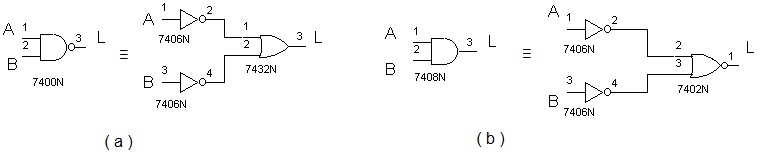
Figura 6 - Obtendo a função NE e E a partir da função OU, NOU e NÃO
3. Experiência: Equivalência entre portas - obtendo o inversor a partir de NE ou NOU
3.1. Abra o arquivo ExpTDC_13_Obtendo_o_Inversor_a_partir_de_NAND_e_NOU e identifique os circuitos da Figura 7. Inicie a simulação e em seguida verifique a equivalencia observando os indicadores (probes) na entrada e saida. Use a chave A para mudar de estado na entrada.
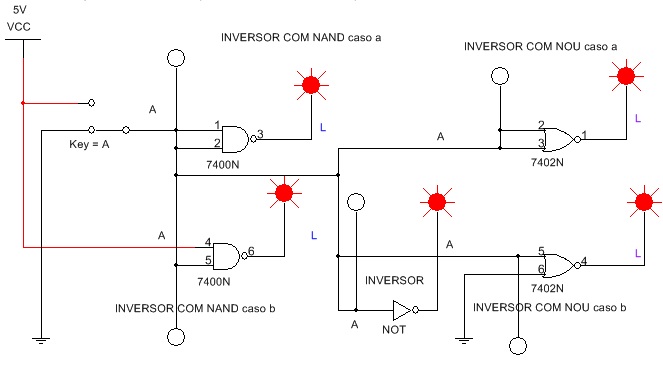
Figura 7 - Obtendo o inversor a partir de NE (NAND) e NOU (NOR)
4. Experiência: Equivalência de Portas - Obtendo NOU e OU partir de NE, E e inversores
4.1. Abra o arquivo ExpTDC_14_Obtendo NOU e OU a partir de NE e inversores e identifique os circuitos da Figura 8. Inicie a simulação e verifique a equivalência entre os circuitos levantando a Tabela Verdade do circuito, tabela 1.
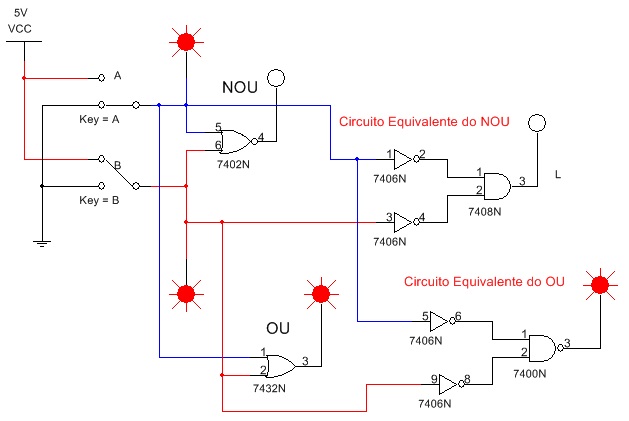
Figura 8 - Obtendo o NOU e OU a partir de NE, E e NÃO
Arquivo Multisim Live
Tabela 1 - Obtendo o NOU e OU a partir de NE, E e NÃO
| Chave B | Chave A | Saida NOU | Saida OU | Saida Equivalente NOU | Saida Equivalente OU |
| 0V | 0V | ||||
| 0V | 5V | ||||
| 5V | 0V | ||||
| 5V | 5V |
4.2. Escreva as suas conclusões.
5. Experiência: Equivalência entre portas - obtendo NE e E partir de OU, NOU e inversores
5.1. Abra o arquivo ExpTDC_15_Obtendo_NE_E_Usando_NOU_OU_inversores e identifique os circuitos da Figura 9. Inicie a simulação e verifique a equivalência entre os circuitos levantando a Tabela Verdade dos circuitos, tabela 2.
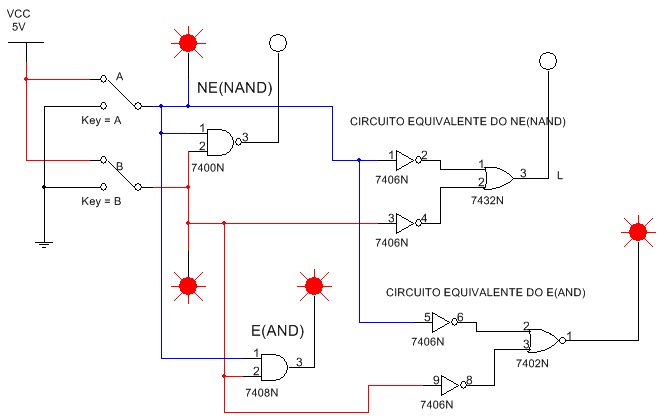
Figura 9 - Obtendo o NE e E a partir de NOU, OU e NÃO
Arquivo Multisim Live
Tabela 2 - Obtendo o NE e E a partir de NOU, OU e NÃO
| Chave B | Chave A | Saida NE | Saida E | Saida Equivalente NE | Saida Equivalente E |
| 0V | 0V | ||||
| 0V | 5V | ||||
| 5V | 0V | ||||
| 5V | 5V |
5.2. Escreva as suas conclusões.
